3

I want to solve $$ \int_{0}^\infty\frac{\log^3(x)}{x^2+1}\,dx=0. $$ The problem is that when I use the curve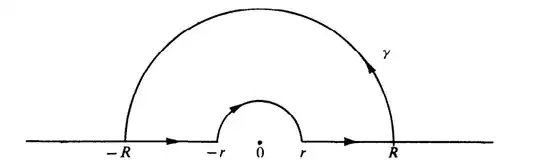enter image description here

I have that \begin{align*} 0 &=\int_{\Gamma}\frac{\log^3 z}{z^2+1}\\ &=\int_{\gamma_r}\frac{\log^3 z}{z^2+1} +\int_{\gamma_R}\frac{\log^3 z}{z^2+1} +\int_{r}^R\frac{\log^3x}{x^2+1} +\int_{-R}^{-r}\frac{(\log|x|+i\pi)^3}{x^2+1} \end{align*} where $\log z$ is the log without negative pure complex numbers. Also ($\rho=R$ or $\rho=r$) \begin{align*} \int_{\gamma_\rho}\frac{\log^3z}{z^2+1} &=\int_0^\pi\frac{(\log\rho+i\theta)^3}{\rho^2e^{2i\theta}+1}i\rho e^{i\theta}\,d\theta =\int_0^\pi\frac{\log^3\rho-i\theta^3+3i\theta\log^2\rho-3i\theta^2\log\rho}{\rho^2e^{2i\theta}+1}i\rho e^{i\theta}\,d\theta\\ &=\int_0^\pi\frac{\log^3\rho}{\rho^2e^{2i\theta}+1}i\rho e^{i\theta}\,d\theta -i\int_0^\pi\frac{\theta^3}{\rho^2e^{2i\theta}+1}i\rho e^{i\theta}\,d\theta +3i\int_0^\pi\frac{\theta\log^2\rho}{\rho^2e^{2i\theta}+1}i\rho e^{i\theta}\,d\theta -3i\int_0^\pi\frac{\theta^2\log\rho}{\rho^2e^{2i\theta}+1}i\rho e^{i\theta}\,d\theta \end{align*} And \begin{align*} \int_{-R}^{-r}\frac{(\log|x|+i\pi)^3}{x^2+1} =\int_{r}^{R}\frac{(\log|x|+i\pi)^3}{x^2+1} =\int_{r}^{R}\frac{\log^3x-i\pi^3+3i\pi\log^2x-3i\pi^2\log x}{x^2+1} \end{align*} But I'm uncertain if this is the way, cause is huge and I don't know how to lead with integration of $\frac{\log^2x}{x^2+1}$.

Kempa
  • 648
  • 3
  • 8
  • 3
    If you don't have to use complex analysis, then you can just observe that the substitution $x = \frac{1}{t}$ shows $I = -I$. – Daniel Schepler Nov 14 '23 at 21:50
  • for god sake @DanielSchepler, bless for you – Kempa Nov 14 '23 at 22:02
  • In the last display equation, you are missing the differentials $dx$, and in the last expression the factor $i$ in the term $-3 i \pi^2 \log x$ shouldn't be there. – Travis Willse Nov 14 '23 at 22:04
  • 1
    If on the other hand you'd wanted $\int_0^\infty\frac{\log^2xdx}{x^2+1}$, which doesn't vanish, a keyhole contour might be easier than a semicircular one, although counterintuitively you'd want to integrate $\frac{\log^3z}{z^2+1}$ around it, because the calculation gets a $\ln^2z$ term from expanding $\ln^3z-(\ln z+2i\pi)^3$. – J.G. Nov 14 '23 at 22:05
  • 1
    It's not quite a duplicate inasmuch as it includes the even exponent case, but this post is relevant: https://math.stackexchange.com/questions/3010205/how-to-solve-int-0-infty-frac-lognx1x2dx – Travis Willse Nov 14 '23 at 22:06

2 Answers2

1

For any positive, odd integer $k$, the substitution $$x = \frac{1}{u}$$ gives $$I := \int_0^\infty \frac{\log^k x}{1 + x^2} = - \int_0^\infty \frac{\log^k u}{1 + u^2} = -I .$$

Remark For even $k$, the integrand is nonnegative everywhere and positive in some places (in fact, everywhere except $x = 1$), so the integral has positive value.

Travis Willse
  • 99,363
0

Since @Travis Willse gave the answer for odd velues of $k$, for the beauty of it $$I := \int_0^\infty \frac{\log^{2k}( x)}{1 + x^2}\,dx =2^{-4 n}\, n\,\Gamma (2 n)\, \left(\zeta \left(2 n+1,\frac{1}{4}\right)-\zeta \left(2 n+1,\frac{3}{4}\right)\right) $$

$$\zeta \left(2 n+1,\frac{1}{4}\right)-\zeta \left(2 n+1,\frac{3}{4}\right)=2 \pi ^{2 n+1}\,\frac {a_n}{b_n}$$ where the $b_n$ form sequence $A360966$ in $OEIS$ (with a shift of $1$) and the $a_n$ form the (unknown ?) sequence $$\{1,5,122,277,101042,1081106,797443924,3878302429,4809759350882\}$$

Even the antiderivatives are not too complicated if you enjoy polylogarithms of complex areguments (coming from $x^2+1=(x+i)(x-i)$ followed by partial fraction decomposition).

Claude Leibovici
  • 260,315