It is well known that :
$$\ \ \ \ \ \ \binom{(A,C;B,D)}{\text{harmonic division}}\ \iff \ \binom{\text{cross-ratio}}{ [A,C;B,D]=-1}.$$
(definition of cross-ratio here).
A non-classical formula in the case where $A,B,C,D$ are aligned in this order, expresses the general (negative) cross-ratio under the form :
$$[A,C;B,D]=-\frac{1}{\tan^2(\tfrac{\theta}{2})}\tag{1}$$
as a function of the angle $\theta$ between circles with resp. diameters $[AC] $ and $[BD]$.
Fig. 1 : Case $a=0,b=2,c=3,d=7$, one gets $[A,C;B,D]=-1/\tan^2(93.82°/2)$.
I provide two proofs of formula (1) below.
I hadn't seen previously this formula until I found it, under a different form (up to Cayley transform $Z=\frac{z-i}{z+i}$) in a recent question to which I haven't answered directly because there was no evidence of work. Unlike this previous question, I do not make reference to hyperbolic geometry.
My questions are : where can be found references to this formula in the literature on projective geometry ? To which other properties can it be connected ?
Proofs of formula (1) :
Proof 1 : (found afterwards, but placed first because it is simpler)
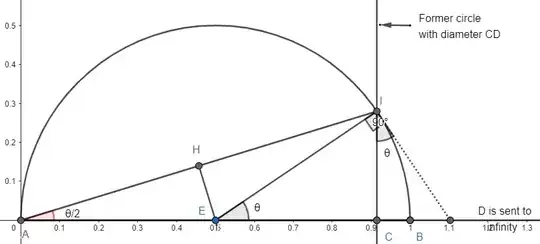
This issue is (classicaly) equivalent to this one (see figure 2), where the coordinates of $A,B,D$ are $0,1,\infty$ resp. More precisely, we keep the left circle as it was and we transform the right circle still making an angle $\theta$ with the first one into a vertical line in $C$, ("circle with an infinite radius").
Fig. 2.
In this way $\angle CEI = \theta$ (mutually orthogonal sides) ; therefore angle $\angle CAI = \theta/2$ (inscribed angle theorem).
As a consequence
$$AH=\tfrac12 \cos \tfrac{\theta}{2} \implies AI=\cos \tfrac{\theta}{2}$$
Then $$AC=\left(\cos \tfrac{\theta}{2}\right)^2$$
The cross ratio is
$$\frac{\overline{CA}}{\overline{CB}}\frac{\overline{DA}}{\overline{DB}} = \frac{-\left(\cos \tfrac{\theta}{2}\right)^2}{1-\left(\cos \tfrac{\theta}{2}\right)^2} \times \frac11$$ $$=-\frac{1}{\left(\tan \tfrac{\theta}{2}\right)^2} $$
Proof 2 : Let lower case letters $a,b,c,d$ be used for the abscissas of $A,B,C,D$ resp.
The angle between two intersecting circles is given by the formula :
$$\cos \theta = \frac{d^2-(r_1^2+r_2^2)}{2 r_1 r_2}\tag{2}$$
where $r_1,r_2$ are the circles' radii and $d$ the distance between the two centers by an immediate application of the law of cosines to triangle $C_1IC_2$ where $I$ is the intersection point of the two half-circles.
With the notations of the figure, (2) can be given the form :
$$\cos \theta = \frac{\left(\tfrac12(b+d)-\tfrac12(a+c)\right)^2-\left(\tfrac12(a-c)\right)^2-\left(\tfrac12(b-d)\right)^2}{2\tfrac12(a-c)\tfrac12(b-d)}$$
Different simplifications yield :
$$\cos \theta = \frac{(a-b)(c-d)+(b-c)(c-a)}{(a-c)(b-d)}$$
$$\cos \theta = \underbrace{[A,D;B,C]}_{\frac{r}{r-1}}-\underbrace{[B,A;C,D]}_{\frac{1}{1-r}}$$
(where $r$ denotes cross-ratio $[A,C;B,D]$). Therefore, we have :
$$\cos \theta = \frac{r}{r-1}-\frac{1}{1-r}= \frac{r+1}{r-1}= \frac{1+\tfrac{1}{r}}{1-\tfrac{1}{r}}.$$
From there, one can deduce formula (1) as a consequence of the following classical formula (see here) :
$$\cos \theta = \frac{1-t^2}{1+t^2} \ \text{where} \ t=\tan(\tfrac{\theta}{2}).$$