Background: the beam case (1D)
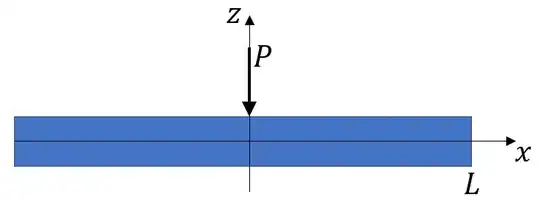
For a beam bearing concentrated froce $P$ at the middle, the concentrated force $P$ can be expressed in a distributed manner, i.e., $$ q=P\delta(r) $$ such that the line integration $$ \int_{-L}^Lqdx=P $$
The circular plate case (2D with axisymmetry)
According to the accepted answer of this post, the concented force $P$ at the center of a circular plate can be expressed as $$ q=\frac{P}{2\pi r}\delta(r) $$ such that the area integration $$ \int_0^Rq\bullet2\pi rdr =P\int_0^R \delta(r)dr=P $$
But I am confused about the value of $q$ in the domain $r\in [0,R]$. Mathematica told me that $$ q(r)=0, {\forall} r {\in} [0,R] $$
It's like that no pressure is applied on the surface of the plate, but somehow it is equivelant to a conentrated force at the center. How to understand this?
