I have this negative number $x<-1$ (thus in the lower branch of the Lambert W function). Is it possible to find $W_{0}(xe^x)$ in terms of $x$ in a useful/non-trivial form?
Asked
Active
Viewed 369 times
1 Answers
2
By the definition of the Lambert W function, the value $y = W_0\left(x \mathrm{e}^{x}\right)$ satisfies:
$$
y \mathrm{e}^{y} = x \mathrm{e}^{x}
$$
There are two real solutions to this equation for each $x<-1$. One $y\leqslant -1$ and another $-1 \leqslant y < 0$. The solutions are $W_{-1}\left(x \mathrm{e}^{x}\right) = x$ and $W_0\left( x \mathrm{e}^{x} \right)$. The latter solution is a non-trivial function of $x$. 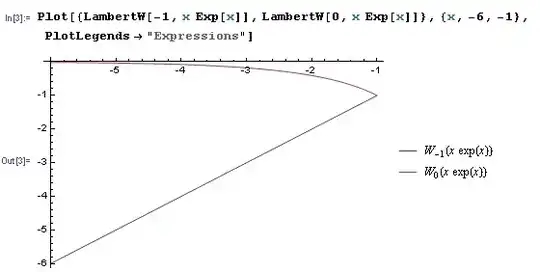
Sasha
- 70,631
-
I understand that the function is non-trivial on x. I meant to ask for some form of expression that is non-trivial/useful. A perfect example of what I think is considered trivial is $W_{0}(xe^x)$. I hope you understand my question better. – resgh Aug 30 '13 at 19:40