Numerical integration on surface in spherical corrdinates

Question

For a simulation I need to integrate in a spherical coordinate system. Currently I check my code by performing the integral on the analytic case. But I failed to calculate the correct solution. The analytic function is defined as $f(r,\theta,\phi)=\frac{1}{r^2}$. Since the analytical integral would be:

$\int_0^{2\pi}\int_0^\pi\frac{1}{r^2}r^2\sin \theta d\theta d\phi=\int_0^{2\pi}2 d\phi=4\pi$.

Now the numerical integral. Say we place us on $r=2$. The sphere is discretized by 100x100 equidistant arc element. Since my element $f_i=0.25$, $\Delta\theta=\frac{r \pi}{100} =0.06346652$, $\Delta\phi=\frac{r 2\pi}{100} =0.12693304$.

For a numerical integral I would use the trapeze rule: $\sum_i^{100}f_i\Delta\theta\Delta\phi$ but this completely wrong and cannot figure out what is the correct proceeding.

Answer 1

The error is that the numerical integral do not provide a discrete sphere surface element. As described here Surface Element in Spherical Coordinates the integral $\int\int f(r,\theta,\phi) r^2 \sin(\theta)d\theta d\phi$. As we see the surface vanishes on both poles. My numerical definition do not take in account that the surface decrease, instead it assume that the sphere surface is composed of square tiles.

$\Delta \theta$ and $\Delta \phi$ are arc elements. Numerically the sum $\sum_i^{100} f_i \Delta \theta$ can be refereed to arc integration such as $\int f(r,\theta,\phi) r d\theta$. There I get the correct solution.

For numerical surface integration I first need a mesh, where the tiles have a specific surface. https://i.stack.imgur.com/3LPIA.jpg

Answer 2

Your problem is most likely in coding. Maybe [StackOverflow] would be a better suit for this question.

In any case, I tried numerical a quick Fortran example with the following results

 Spherical Surface Integral (         100 ,         100 )
 Expect:    12.5663706143592      (   4.00000000000000      pi)
 Actual:    12.5668874005135      (   4.00016449814196      pi)

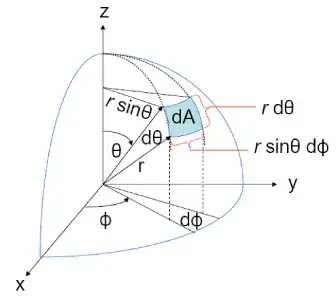
The full program below uses the f_inv_sq(r,u,v) function to return $f(r,u,v)=\tfrac{1}{r^2}$ and S_integral_spherical(f,r,n,m) to do the numerical integration of function f(r,u,v) over the surface of a sphere using n and m subdivisions of the angles.

program FortranConsole2
use, intrinsic :: iso_fortran_env
implicit none

integer, parameter :: wp = real64

interface
    function V_scalar(r,u,v) result(f)
    import
    real(wp), intent(in) :: r,u,v
    real(wp) :: f
    end function
end interface

real(wp), parameter :: pi = acos(-1.0d0)

! Variables
real(wp) :: r, f, f_expect
integer :: n,m

r = 2.0_wp
n = 100
m = 100

print *, "Spherical Surface Integral (",n,",",m,")"
f_expect = 4*pi
f = S_integral_spherical(f_inv_sq, r, n, m)
print *, "Expect: ", f_expect, "(", f_expect/pi,"pi)"
print *, "Actual: ", f, "(", f/pi,"pi)"

contains

function S_integral_spherical(f,r,n,m) result(s)
real(wp) :: s
procedure(V_scalar),intent(in),pointer :: f
real(wp), intent(in) :: r
integer, intent(in) :: n,m
integer :: i,j
real(wp) :: ds, u, v, du, dv

s = 0.0_wp
du  = (2*pi)/n
dv = (pi)/m
do i=1, n
    u = (i-0.5_wp)*du
    do j=1, m
        v = (j-0.5_wp)*dv
        ds = r**2*sin(v)*du*dv
        s = s + f(r,u,v)*ds
    end do
end do
end function

function f_inv_sq(r,u,v) result(f)
real(wp), intent(in) :: r,u,v
real(wp) :: f
    f = 1/r**2
end function

end program

The crux of the above is the double loop for i and j inside, which accumulates the surface integral value s using

ds = r**2 * sin(v) * du * dv
s = s + f(r,u,v) * ds

where v represents the angle $\theta$ in your post, and u the angle $\varphi$.

or mathematically

$$ {\rm d}s = r^2 \sin \theta\,{\rm d}\theta\,{\rm d}\varphi $$

$$ s = \int f(r,\varphi,\theta)\,{\rm d}s$$