I have come across this sum:
$$\sum\limits_{n=1}^{N-1} \frac{(-1)^n}{\sqrt{1-\cos{\frac{2\pi n}{N}}}} $$
where $N$ is an even integer (it evaluates to $0$ for odd $N$). How does one evaluate this sum (or approximate its answer)? The only reason I ask is that, after plotting it in python, the answer seems to be of the form $aN + b$ for some constants $a$, $b$, which suprised me.
Any help or tips on how to go about this problem would be greatly appreciated.
We can try to get the full asymptotics of the sum $\,\,S_N=\displaystyle \sum\limits_{n=1}^{N-1} \frac{(-1)^n}{\sqrt{1-\cos{\frac{2\pi n}{N}}}}\,\,$ at $\,\,N\to\infty$ $$S_N=\frac1{\sqrt2}\sum\limits_{n=1}^{N-1} \frac{(-1)^n}{\sin{\frac{\pi n}{N}}}$$ Now let's go in the complex plane and consider the integral $\,\,\displaystyle I_C=\frac{1}{\sqrt2\,2\pi i}\oint_C\frac{\pi}{\sin\pi z}\frac{dz}{\sin\frac{\pi z}N}\,\,$ along the following rectangular contour with two added arches of the small radius $\,\pi\epsilon\,$ (around $z=0$ and $z=N$, clockwise)
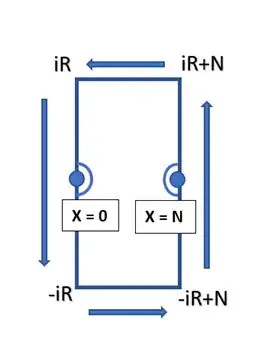
There are $N-1$ poles inside the contour (at $z=1, 2, ...N-1$). Evaluating residues of the integrand, we get $$I_C=\frac1{\sqrt2}\sum\operatorname{Res}\frac{\pi}{\sin\pi z}\frac1{\sin\frac{\pi z}N}=S_N$$ On the other hand, leading $R\to\infty$, using the fact that $N$ is even and making the substitution $z=ix/\pi$ $$I_C=\frac{2\sqrt2i}{2\pi i}\int_\epsilon^\infty\frac{dx}{\sinh x\sinh\frac xN}+I_{C_\epsilon}\tag{1}$$ where the integral along the arches $$I_{C_\epsilon}=\frac{\sqrt2i}{2\pi i}\int_\pi^0\frac{\epsilon e^{i\phi}id\phi}{\sinh(\epsilon e^{i\phi})\sinh\frac{\epsilon e^{i\phi}}N}=\frac{N}{\pi \epsilon\sqrt2}\int_\pi^0e^{-i\phi}id\phi+O(\epsilon)=-\frac{\sqrt2\,N}{\pi\epsilon }+O(\epsilon)\tag{2}$$ From (1) and (2) follows $$S_N=\frac{\sqrt2}{\pi}\left(\int_\epsilon^\infty\frac{dx}{\sinh x\sinh\frac xN}-\frac N\epsilon\right)+O(\epsilon)=\frac{\sqrt2\,N}{\pi}\int_\epsilon^\infty\left(\frac1{N\sinh x\sinh\frac xN}-\frac 1{x^2}\right)dx+O(\epsilon)$$ The integrand is regular at $x\to0$; therefore, leading $\epsilon \to 0$ $$S_N=\frac{\sqrt2\,N}{\pi}\int_0^\infty\left(\frac1{N\sinh x\sinh\frac xN}-\frac 1{x^2}\right)dx\tag{3}$$ Just to draw the attention to the fact that this is an exact formula for the sum; from here we can derive as many asymptotic terms as we want.
Decomposing $\,\sinh\frac xN\,$ in the first term ($N\to\infty$) $$S_N=\frac{\sqrt2\,N}{\pi}\left(\int_0^\infty\left(\frac1{\sinh x}-\frac1x\right)\frac{dx}x-\frac1{6N^2}\int_0^\infty\frac x{\sinh x}dx\right)+O\Big(\frac1{N^3}\Big)\tag{4}$$ The first integral can be evaluated by means of analytical continuation (other approaches are, for example, here or here) $$\int_0^\infty\left(\frac1{\sinh x}-\frac1x\right)\frac{dx}x=-\ln2\tag{4a}$$ The evaluation of the second integral is straightforward: $$\int_0^\infty\frac x{\sinh x}dx=\int_0^\infty\left(\frac1{e^x-1}+\frac1{e^x+1}\right)xdx=\Gamma(2)\Big(\zeta(2)+\eta(2)\Big)=\frac{\pi^2}4\tag{4b}$$ Putting (4a) and (4b) into (4) $$S_N=-\,\frac{\sqrt2\ln2}{\pi}N-\frac\pi{12\sqrt2}\frac1N+O\Big(\frac1{N^3}\Big)$$ Numeric check confirms the result. The full asymptotics can also be obtained.
To note that the first (linear) term can be easily obtained by means of the approximation proposed by @J.G. in the comment.
I shall derive a complete asymptotic expansion with an estimate for the remainder term starting with Svyatoslav's integral formula for your sum $S_N$. From Svyatoslav's answer $$ S_N = \frac{{\sqrt 2 N}}{\pi }\int_0^{ + \infty } {\left( {\frac{1}{{\sinh x}}\frac{{x/N}}{{\sinh (x/N)}} - \frac{1}{x}} \right)\!\frac{{{\rm d}x}}{x}}. $$ Now for any $t>0$ and $M\ge 1$, we have $$ \frac{t}{{\sinh t}} = 1 + \sum\limits_{m = 1}^{M - 1} {\frac{{2(1 - 2^{2m - 1} )B_{2m} }}{{(2m)!}}t^{2m} } + \Theta _M (t)\frac{{2(1 - 2^{2M - 1} )B_{2M} }}{{(2M)!}}t^{2M} $$ where the $B_m$ denote the Bernoulli numbers and $0<\Theta _M (t)<1$ (see Lemma $2.2$ in this paper). Thus, using the mean value theorem for improper integrals, \begin{align} S_N = \, &\frac{{\sqrt 2 N}}{\pi }\int_0^{ + \infty } {\left( {\frac{1}{{\sinh x}} - \frac{1}{x}} \right)\!\frac{{{\rm d}x}}{x}} \\& + \frac{{\sqrt 2 }}{\pi }\sum\limits_{m = 1}^{M - 1} {\frac{{2(1 - 2^{2m - 1} )B_{2m} }}{{(2m)!}}\int_0^{ + \infty } {\frac{{x^{2m - 1} }}{{\sinh x}}{\rm d}x} \frac{1}{{N^{2m - 1} }}} \\& + \theta _M (N)\frac{{\sqrt 2 }}{\pi }\frac{{2(1 - 2^{2M - 1} )B_{2M} }}{{(2M)!}}\int_0^{ + \infty } {\frac{{x^{2M - 1} }}{{\sinh x}}{\rm d}x} \frac{1}{{N^{2M - 1} }}, \end{align} where $0<\theta _M (N)<1$. Now from Svyatoslav's answer $$ \int_0^{ + \infty } {\left( {\frac{1}{{\sinh x}} - \frac{1}{x}} \right)\frac{{{\rm d}x}}{x}} = - \log 2. $$ Using the Riemann Zeta function, we find \begin{align} \int_0^{ + \infty } {\frac{{x^{2m - 1} }}{{\sinh x}}{\rm d}x} & = 2(2m - 1)!(1 - 2^{ - 2m} )\zeta (2m) \\ & = ( - 1)^{m + 1} \frac{{\pi^{2m} (2^{2m}-1 )}}{{2m}}B_{2m} . \end{align} Accordingly, \begin{align} S_N = - \frac{{\sqrt 2 \log 2}}{\pi }N & + \sum\limits_{m = 1}^{M - 1} {( - 1)^m \frac{{\pi ^{2m - 1} (2^{2m} - 1)(2^{2m} - 2)B_{2m}^2 }}{{\sqrt 2 m(2m)!}}\frac{1}{{N^{2m - 1} }}} \\ & + \theta _M (N)( - 1)^M \frac{{\pi ^{2M - 1} (2^{2M} - 1)(2^{2M} - 2)B_{2M}^2 }}{{\sqrt 2 M(2M)!}}\frac{1}{{N^{2M - 1} }} \end{align} for any $N\ge 2$, $M\ge 1$ with a suitable $0<\theta _M (N)<1$.