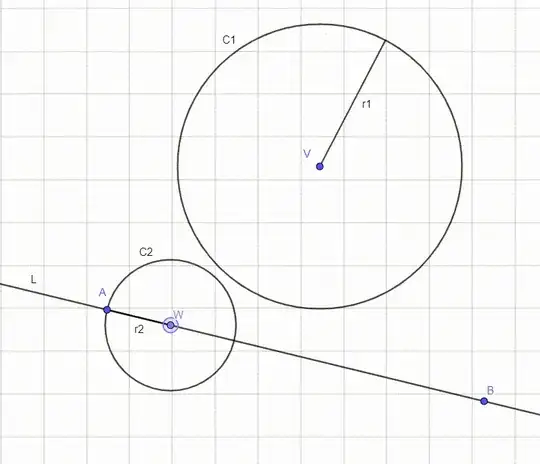
I've been struggling to find a way to resolve the following problem:
Let $C_1$ a circle of center $V$ and of radius $r_1$. Let $A$ and $B$ two points outside of $C_1$, and $L$ a line passing by them. Let $W$ a point on $L$. Let $C_2$ a circle of center $W$ passing through $A$ (radius $r_2$ is the distance between $A$ and $W$).
I am looking for the coordinate of the point $W$ so that $C_2$ intersects $C_1$ in a single point (that is that $C_1$ and $C_2$ are externally tangent).
What do you think? I tried to visualize a logic behind it using GeoGebra but couldn't figure it out. Right now what I'm doing in my code (this is for generative design) is increasing the distance between $A$ and $W$ by small steps until the distance $VW$ is equal to $r_1 + r_2$, but I'm looking for the elegant, geometrical solution!