0

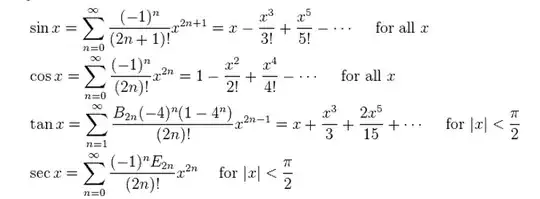
Here's what i want to know,how does sinx and cosx equals such taylor series?

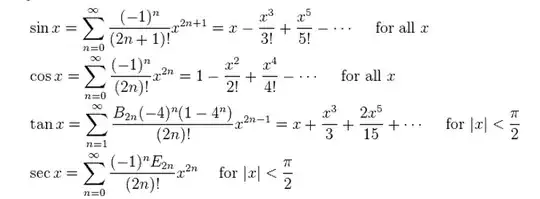
Any proof or derivation for the sinx and cosx function would be help. Image taken from http://en.wikipedia.org/wiki/Taylor_series

abhishek khandal
  • 13
  • Calculate the derivatives of $;\sin x,,,\cos x,;$ etc., evaluate in zero and...voila! – DonAntonio Aug 29 '13 at 11:05
  • Hint: $\sin'(x) = \cos(x), \cos'(x) = -\sin(x)$. Use Taaylor's theorem for the rest. – AlexR Aug 29 '13 at 11:06
  • 2
    You can find the derivations in any college-level analysis textbook. –  Aug 29 '13 at 11:06
  • ..."in any analysis textbook..." and in hundreds, or thousands, of internet sites. – DonAntonio Aug 29 '13 at 11:06
  • You might find this answer illuminating. It shows the geometric nature of the terms of the power series. (The linked note of mine has a reference to a combinatorial proof for sine and cosine; the note itself covers a slightly-more-involved combinatorial proof for secant and tangent.) – Blue Aug 29 '13 at 11:53

1 Answers1

0

You can find proofs in this book. (chapter 6 for $\tan(x)$ and $\sec(x)$). For $\sin(x)$ and $\cos(x)$ you must use Taylor theorem.

user91500
  • 5,606
  • 2
    So: the advice becomes... after you see some Taylor series given on the internet, and become curious: Go to a textbook (or course) and learn enough calculus to discover what Taylor's theorem says. – GEdgar Aug 29 '13 at 11:53