When will $AB=BA$?

Question

Given two square matrices $A,B$ with same dimension, what conditions will lead to this result? Or what result will this condition lead to? I thought this is a quite simple question, but I can find little information about it. Thanks.

Since everybody (except Hauke) is just listing their favorite sufficient conditions let me add mine: If there exists a polynomial $P\in R[X]$ ($R$ a commutative ring containing the entries of $A$ and $B$) such that $B=P(A)$, then we have $AB=BA$. Furthermore, in the case that $R$ is (contained in) an algebraically closed field and the eigenvalues of $A$ are distinct, then this sufficient criterion is also necessary. For more read the Wikiarticle linked to by Hauke. — Jyrki Lahtonen, Aug 29 '13 at 08:17

score 11 · Accepted Answer · edited Apr 13 '17 at 12:21

If $A,B$ are diagonalizable, they commute if and only if they are simultaneously diagonalizable. For a proof, see here. This, of course, means that they have a common set of eigenvectors.

If $A,B$ are normal (i.e., unitarily diagonalizable), they commute if and only if they are simultaneously unitarily diagonalizable. A proof can be done by using the Schur decomposition of a commuting family. This, of course, means that they have a common set of orthonormal eigenvectors.

score 10 · Answer 2 · edited Nov 17 '17 at 05:03

10

Here are some different cases I can think of:

$A=B$.
Either $A=cI$ or $B=cI$, as already stated by Paul.
$A$ and $B$ are both diagonal matrices.
There exists an invertible matrix $P$ such that $P^{-1}AP$ and $P^{-1}BP$ are both diagonal.

edited Nov 17 '17 at 05:03

Community

1

answered Aug 29 '13 at 07:31

Ryan

1,389

2
$A=cB$ or $A=cB^{-1}$ or $B=0$

ryang

Feb 03 '21 at 02:50

score 9 · Answer 3 · answered Aug 29 '13 at 07:17

This is too long for a comment, so I posted it as an answer.

I think it really depends on what $A$ or $B$ is. For example, if $A=cI$ where $I$ is the identity matrix, then $AB=BA$ for all matrices $B$. In fact, the converse is true:

If $A$ is an $n\times n$ matrix such that $AB=BA$ for all $n\times n$ matrices $B$, then $A=c I$ for some constant $c$.

Therefore, if $A$ is not in the form of $c I$, there must be some matrix $B$ such that $AB\neq BA$.

Ziyuan · Answer 4 · 2019-01-04T11:56:50.987

There is actually a sufficient and necessary condition for $M_n(\mathbb{C})$:

Let $J$ be the Jordan canonical form of a complex matrix $A$, i.e., $$ A=PJP^{-1}=P\mathrm{diag}(J_1,\cdots,J_s)P^{-1} $$ where $$ J_i=\lambda_iI+N_i=\left(\begin{matrix} \lambda_i & & &\\ 1 & \ddots & & \\ & \ddots & \ddots & \\ & & 1 & \lambda_i \end{matrix}\right). $$ Then the matrices commutable with $A$ have the form of $$ B=PB_1P^{-1}=P(B_{ij})P^{-1} $$ where $B_1=(B_{ij})$ has the same blocking as $J$, and $$ B_{ij}=\begin{cases} 0 &\mbox{if } \lambda_i\ne\lambda_j\\ \mbox{a }\unicode{x201C}\mbox{lower-triangle-layered matrix''} & \mbox{if } \lambda_i=\lambda_j \end{cases} $$

The reference is my textbook of linear algebra, though not in English. Here is an example in the book:

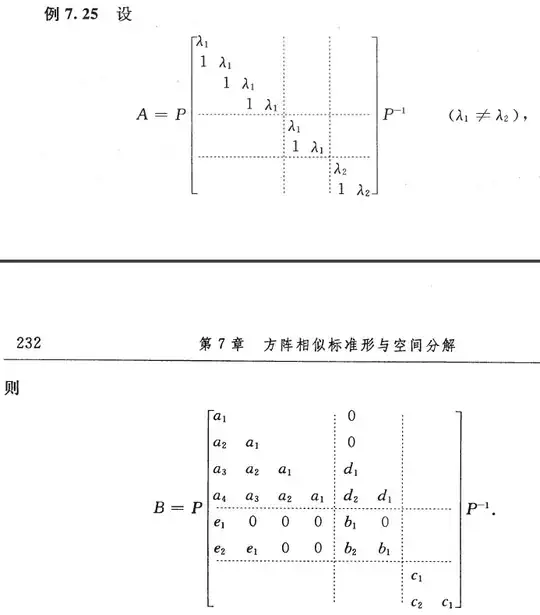
enter image description here

The main part in the proof is to compare the corresponding entries in both sides of the equation $N_iB_{ij}=B_{ij}N_j$ when $\lambda_i=\lambda_j$.

When will $AB=BA$?

4 Answers4

Linked

Related