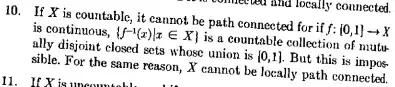Dugundji: cofinite topology on countable infinite set is totally path-disconnected

Question

In James Dugundji's Topology (1966), chapter V, are the following problems:

1.3 Let $X$ be a[n infinite] countable set, with topology $\cal T = \{\emptyset\} \cup \{ A \space \vert \space {\complement}A$ is finite$\}$. Show that $X$ is connected.

5.3 Let $X$ be the connected set in 1, Problem 3. Show that $X$ is totally pathwise disconnected. (By definition, $X$ is called totally pathwise disconnected if the only continuous maps $f: I \to X$ are the constant maps.)

The first one is easy: in the cofinite topology, any two nonempty open sets meet, so there's no disconnection of $X$.

The second one was a challenge for me. A path in $X$ must be compact and connected, but all subsets of $X$ are compact and connected, so that doesn't help. Eventually I realized that a map $f: A \to X$ is continuous precisely when all fibers $f^{-1}(x)$ are closed. That led me to Proving a Sierpiński result on partitions of the unit interval into closed sets.

So that's an answer, but it's hard for me to imagine many beginning topology students getting it. At this point in the text, we haven't even seen compactness, or identification maps, or separation axioms. Here's someone on Math Overflow who also found it not trivial: Why are the integers with the cofinite topology not path-connected?.

Possibly there's a mistake in the text that makes this problem unusually hard? Certainly it has many small mistakes (you can see where I had to apply a correction above to Problem 1.3).

Question. Is there any simpler approach to Problem V.5.3?

I got interested in this question because of a resemblance to the pseudo-arc, which is another space with a homogeneous feel that's connected but totally path-disconnected. The pseudo-arc is Hausdorff, though, which makes it pretty different. So, a bonus question: are there other interesting examples of such spaces?

Answer 1

I do not think there is a simpler way to prove this exercise, and the reason is that the conclusion of this exercise implies (and is hence equivalent to) Sierpiński's result.

In other words, if, contrary to Sierpiński, we have a nontrivial decomposition of $[0,1]$ into disjoint closed sets $\{A_i\}$ then we may define $f\colon [0,1]\to \mathbb N$ by $f(x)=i$ for $x\in A_i$. Then the inverse image of every finite set is closed, hence $f$ is a continuous and nonconstant map, contradicting the conclusion of the exercise.

Therefore a simple proof for the exercise would give a simple proof for Sierpiński's theorem itself.

Answer 2

The proof you describe is essentially what's used by Steen and Seebach in Counterexamples (though something about non-emptyness should have been clarified):

I agree that's flexing somewhat heavy muscle. But let's consider the fact that the co-finite topology on a set of cardinality $\mathfrak c$ is path-connected. So any proof necessarily relies on the cardinality at play here.