How to treat dx in my logic of Fundamental Theorem of Calculus

Question

After reading some of the comments and from outside help I've been made aware that my notation may have been the problem. So I'm rewriting this with a new set of questions with better notation and hopefully better understanding.

Let me start from the very beginning - Limits: $\lim_{x\to a} x$ refers to making x very small and almost $a$ but $x\ne a$

The next thing is derivation. Derivative of $f(x)$ if the limit exists refers to the new function $f'(x)$ whose each input $x$ maps to $f$ and output is the slope at that point in the $f$. In other words, the ratio of infinitely small change in $y$ when infinitely small change happens to input $x$ for every point. Mathematically,

$$ \lim_{\triangle x \to 0}\frac{f(x + \triangle x) - f(x)}{\triangle x} $$

Indefinite integral in simpler words is just the opposite of derivative. If the derivative of $f(x)$ is $f'(x)$ then the integral of $f'(x)$ is $f(x) + C$ where $C$ can be any constant which is shown by pushing the curve up or down the slope doesn't change so all $C$ would make the derivative same as $f'(x)$

$$ \int f'(x) = f(x) + C \ \ \ \ \& \ \ \ \ \frac{\mathrm{d}f(x)}{\mathrm{d}x} = f'(x)$$

Problem come in Definate Intregal. To my understanding Definite integral is integral between fixed range $[\alpha, \beta]$ given function is continuous. This solves our problem of $C$ constant as per how it is calculated. According to Theoram:

$$ \int_\alpha^\beta f'(x) = f(\beta) - f(\alpha) $$

which makes sense as:

$$ \begin{align} & \ \ \ \ \ (f(\beta) + C) - (f(\alpha) + C) \\ &= f(\beta) - f(\alpha) + (C-C) \\ &= f(\beta) - f(\alpha) \end{align} $$

Q1. But why is it $f(\beta) - f(\alpha)$ in the first place?

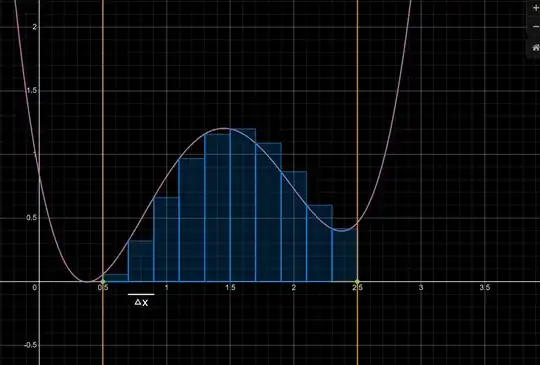
Now I would also want to talk about Area. To get the Area of the curve we divide it into little rectangles with the width of $\triangle x$ which tends to 0 bur $\triangle x \ne 0$

Mathematically area will be:

$$ A() = \lim_{\triangle x \to 0} \triangle x \sum_{i=\alpha}^\beta f(x_i + (i-1)\triangle x) $$

Since from pic $\alpha = 0.5\ \ \beta = 2.5$ the above equation is:

$$ A() = \lim_{\triangle x \to 0} \triangle x \sum_{i=0.5}^{2.5} f(x_i + (i-1)\triangle x) $$

This equation by definition of integration is:

$$ \int_{\alpha}^\beta f(x) \triangle x $$

Now Fundamental Theorem of Calculus says

$$ \int_{\alpha}^\beta f(x) \triangle x = F(\beta) - F(\alpha),\ \ F'(x) = f(x) $$

Q2 - 3:

Q2. What is the relation of Area to antiderivative function?

Q3. How one thus comes to the logic of Subtracting from a geometrical perspective, here above image.

Answer 1

Using the geometric interpretation, $\int_a^b f(z) dz$ is the total signed area between $f$ and the $x$-axis, where we show this intuition as the limit of Riemann sums.

Now, let's replace $b$ with a variable $x>a$ and ask what is the rate of change of the area under the curve at $x$:

$$\frac{d}{dx}\int_a^x f(z) dz = \lim_{h\to0^+} \frac{\int_a^{x+h} f(z) dz - \int_a^x f(z) dz}{h} = \lim_{h\to0^+} \frac{\int_x^{x+h} f(z) dz}{h}$$

$$=\lim_{h\to0^+} \frac1h\left[ \lim_{n\to \infty}\sum_{i=0}^n f\left(x+i\frac hn\right)\frac hn\right] = \lim_{h\to0^+}\left[ \lim_{n\to \infty}\frac1n\sum_{i=0}^n f\left(x+i\frac hn\right)\right]$$

Note that the inner sum is just the mean value of the terms in the sum and the inner limit defines the following Riemann integral:

$$\lim_{n\to \infty}\frac1n\sum_{i=0}^n f\left(x+i\frac hn\right) = \frac1h \int_x^{x+h}f(z)dz$$

Which is mean value of $f$ over $[x,x+h]$

In general if $f$ is integrable over $[a,b]$ then the function $F(x):= \int_a^x f(z)dz$ is uniformly continuous on $[a,b]$ and $F(a)=0$ so $\lim_{x \to a^+} F(x)=0$

Using this, we can switch the limits in the final sum:

$$\lim_{h\to0^+}\left[ \lim_{n\to \infty}\frac1n\sum_{i=0}^n f\left(x+i\frac hn\right)\right] = \lim_{n\to\infty}\left[ \lim_{h\to 0^+}\frac1n\sum_{i=0}^n f\left(x+i\frac hn\right)\right] $$ $$= \lim_{n\to\infty}\left[ \frac1n\sum_{i=0}^n f(x)\right]=\lim_{n\to\infty}f(x) = f(x)$$

So the rate of change in the area of the definite integral at $x$ is $f(x)$, as we expect.