Is there a formula that gives the number of compositions of length $k$ of a number $n$ containing numbers no higher than $p$?

Question

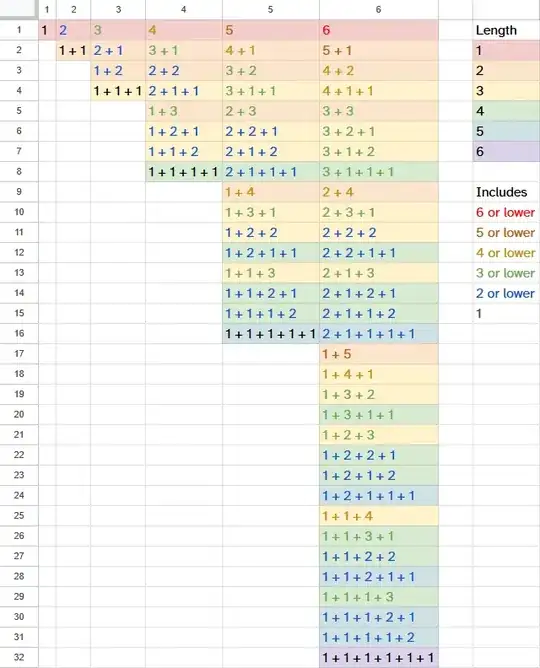
A composition of a positive integer $n$ is a way of writing $n$ as the sum of an ordered sequence of strictly positive integers. Any positive integer $n$ has $2^{n - 1}$ distinct compositions.

Compositions of $n$ range in length from one ($n$ on its own) to $n$ ($n$ instances of the number $1$ added together). The number of compositions of $n$ into exactly $k$ parts is the binomial coefficient $\binom{n - 1}{k - 1}$, or $\frac{(n - 1)!}{(k - 1)! × (n - k)!}$.

What I want to find is a formula that gives the number of compositions of $n$ of length $k$ containing only numbers between $1$ and $p$, inclusive, but no higher.

For example, the number $6$ has $2^{6 - 1} = 32$ compositions: one of length $1$, five of length $2$, ten of length $3$, ten of length $4$, five of length $5$, and one of length $6$. If the cutoff value is $p = 3$, that is reduced to $24$ compositions: zero of length $1$, one of length $2$, seven of length $3$, ten of length $4$, five of length $5$, and one of length $6$.

When $\frac{n}{2} ≤ p ≤ n$, I found that the formula $\binom{n - 1}{k - 1} - k × \binom{n - p - 1}{k - 1} = \frac{(n - 1)!}{(k - 1)! × (n - k)!} - k × \frac{(n - p - 1)!}{(k - 1)! × (n - p - k)!}$ works. However, when $1 ≤ p < \frac{n}{2}$, this formula over-counts the compositions to be excluded. This seems to be because the second term counts, for example, how many numbers greater than $p$ are in compositions of length $k$ and not what I want, which is how many compositions of length $k$ contain at least one number greater than $p$. This means that it double-counts compositions that contain two instances of an invalid number, triple-counts compositions that contain three instances, and so on.

Is it possible to find a closed-form (non-recursive, non-infinite) formula that gives the results I want?

For reference, here are the compositions of integers $1$ through $6$, color-coded by length (background color) and highest number (text color):

Answer 1

The best tool for this sort of thing is generating functions. The answer is the coefficient of $x^n$ in the product

$$(x + x^2 + \dots + x^p)^k.$$

(You can see this very directly by writing down what a term in this product is when fully expanded, it is exactly a composition of the desired sort.) You can interpret this as telling you how many ways there are to get a certain sum of dice rolls when rolling $k$ different $p$-sided die, each of which is labeled with the numbers $\{ 1, \dots p \}$, so when $p = 6$ this tells you about rolling ordinary die. That makes this question a duplicate of other questions - this has been asked many times before - although not obviously. You can simplify the generating function by rewriting it as

$$x^k \left( \frac{1 - x^p}{1 - x} \right)^k.$$

The numerator can be expanded using the binomial theorem while the denominator can be expanded using the binomial theorem with negative exponent; this gives

$$(1 - x^p)^k = \sum_{i=0}^k (-1)^i {k \choose i} x^{pi}$$ $$\frac{1}{(1 - x)^k} = \sum_{j \ge 0} {-k \choose j} (-1)^j x^j = \sum_{j \ge 0} {k+j-1 \choose j} x^j$$

and multiplying these gives

$$x^k \left( \sum_{i, j} (-1)^i {k \choose i} {k + j - 1 \choose k - 1} x^{pi+j} \right)$$

so that the final answer is

$$\sum_{pi+j=n-k} (-1)^i {k \choose i} {k+j-1 \choose k-1} .$$

Whether this counts as a "closed form" is up to you but I don't think it gets any better than this. This may be a little easier to understand as a sum over $i$, namely

$$\boxed{ \sum_{i=0}^{\lfloor \frac{n-k}{p} \rfloor} (-1)^i {k \choose i} {n-pi-1 \choose k-1} }.$$

The $i = 0$ term is ${n-1 \choose k-1}$ which is the answer with no restrictions on $p$. The $i = 1$ term is the first correction term $- k {n-p-1 \choose k-1}$ coming from inclusion-exclusion which you've found already. The subsequent terms are further corrections needed to complete the inclusion-exclusion argument (but personally I prefer to let generating functions do these arguments for me).