2

Let $a,b \in \mathbb{N}$, and $X^a - 1, X^b - 1 \in K[X]$. Then $(X^a -1, X^b - 1) = X^{(a,b)}-1$, where $ (\alpha,\beta)$ is the GCD of $\alpha$ and $\beta$.

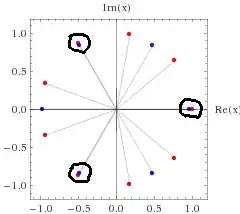
I have an intuitive understanding of this when $K=\mathbb{C}$, given that the roots of $X^a-1$ form a regular polygon around $(0, 0)$ and the GCD's roots would be the "overlapping" points of the two polygons (see below), but I have no idea where to begin proving this for any $K$.

Below are plotted the complex roots of $X^9 - 1$ (red) and $X^6-1$ (blue). There are three overlapping points, and $(X^9-1, X^6-1) = X^3-1$.

complex roots of X^9-1 and X^6-1

I'd appreciate any hints for proving this.

Gabi Purcaru
  • 671

1 Answers1

4

The Euclidean algorithm to compute $\gcd(a,b)$ can be described as follows:

  • If $a<b$ swap $a\leftrightarrow b$ and restart
  • If $b=0$ terminate with $a$ as result.
  • Set $a\leftarrow a-b$ and restart

If $a>b$ note that $$X^a-1=(X^b-1)X^{a-b}+(X^{a-b}-1),$$ hence every step of the Euclidean algorithm used to compute the gcd of $a$ and $b$ is reflected in polynomials of the form $X^n-1$.

Hagen von Eitzen
  • 374,180