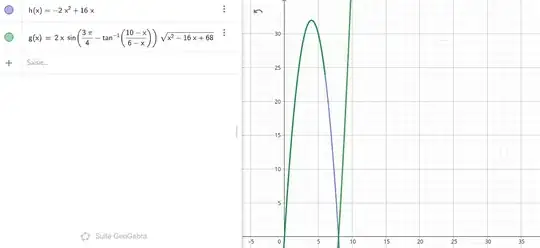
I came up with this formula for computing an area $A$ as a function of $x \in (0,6)$: $$A(x) = 2x\sin\left(\frac{3 \pi}{4}-\arctan\left(\frac{10-x}{6-x}\right)\right)\sqrt{x^2-16x+68}$$
And I want to show that, for $x \in (0,6)$: $$A(x) = -2x^2+16x$$
As you can see in the picture below, it seems to be true.
However, I don't know how to prove it.