My friend showed me this problem from Twitter and I am struggling to solve it. I see that I can manipulate it into several equations (some of which I'll insert below), but none seem to be any progress and I feel like I need a different approach. How do I solve this problem?
$$2x\ln\left(2\right)+\ln\left(\ln\left(x\right)\right)=\ln\left(\ln2\right)+\ln\left(2\right)$$
$$2^{2x-1}\ln x=\ln2$$
$\def\B{\operatorname B}$
$$x^{4^x}=4\iff 4^{4^{-x}}=e^{\ln(4)e^{-\ln(4)x}}=x$$
Now use the Bell polynomial and
How to solve $x^{y^z}=z$: $$e^{ae^{bz}}=z=1+\frac1b\sum_{n=1}^\infty \frac{(ae^b)^n}{nn!}\B_n(b n)$$
with $a=-b=\ln(4)$. The other formula in the post diverges, but the above one works. Therefore:
$$\bbox[4px,border: 4px ridge skyblue]{x^{4^x}=4\iff x=\sum_{n=1}^\infty\frac{\ln^{n-1}(\sqrt2)}{4nn!}\B_n(-n\ln(4))}$$
which matches the digits from @Peter’s comment
When you properly wrote $$2^{(2x-1)}\log( x)=\log(2)$$ you made the function much more linear than the original one and this is very good for any root finding method.
By inspection, you know the the solution is much closer to $1$ than to $2$. So, without resorting to numerical method, make a series expansion around $x=1$, truncate to some order (here, I used the expansion to $O((x-1)^5)$) and use power series reversion to get $$x=1+\frac{L}{2}+\frac{L^2}{8}-\frac{23 L^3}{48}-\frac{143 L^4}{384}+\frac{29 L^5}{48}+L^6-\frac{4 L^7}{3}+O\left(L^{8}\right)$$ where $L=\log(2)$.
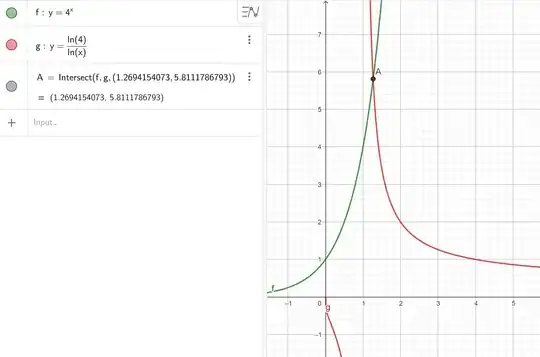
This would give $x=1.266171$ which is not fantastic.
But we can make it up to any order and get better and better results. For example, expanding to $O((x-1)^{15})$ the result would be $\color{red}{1.269}36$
We could do it simpler using, instead of Taylor series, simple Padé approximant. A very simple one is $$2^{(2x-1)}\log( x)\sim P_2=\frac{2 (x-1)+\frac{32 L^3-24 L^2-4 L-1 }{(24 L^2-12 L-1)}(x-1)^2 } {1-\frac{32 L^3-24 L^2+6 L+1}{(24 L^2-12 L-1)} (x-1)+\frac{96 L^4-96 L^3+36 L^2+12 L-1}{6 \left(24 L^2-12 L-1\right)}(x-1)^2 }$$ whose error is $\frac{88}{101} (x-1)^5$.
Now writing $$\text{rhs}=L$$ we have an approximate solution at the price of a simple quadratic equation in $(x-1)$. This would give $x=1.27011$.
Using $P_3$ (whose error is $\frac{3}{106} (x-1)^7$ ) would require the solution of a cubic equation in $(x-1)$. This would give $x=\color{red}{1.26941}63$.
One to approach this is to let $y=4^x$. That's a nice exponential curve that you can plot easily enough on any graph plotter.
That leaves you with $x^y=4$
Taking logarithms gives you $y \ln x=\ln 4$ or $y=\frac{\ln 4}{\ln x}$. Not so nice, but again, it's a curve that you can plot.
Where the two curves intersect will be the solution to your question.
It's not an algebraic method, but it gives you some insight into what's going on.
