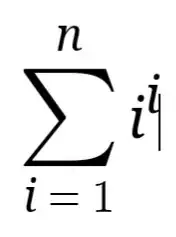How to find the summation of the above series upto $n$ terms?

Asked Sep 26 '23 at 16:48

Active Oct 01 '23 at 00:01

Viewed 66 times

I don't know how to find the summation of the above series upto $n$ terms? I know how to find the summation of the series's like $1^2+2^2+3^2+\ldots+n^2$, $1^3+2^3+3^3+\ldots n^3$? The formula of the summation of the 1st series upto $n$ terms is $n(n+1)(2n+1)/6$ and the formula for the summation of the second series upto $n$ terms is $\left(\dfrac{n(n+1)}{2}\right)^2$. But I don't know how to find the summation of the series $1+2^2+3^3+\ldots n^n$? Please help me out.

edited Oct 01 '23 at 00:01

TShiong

1,257

asked Sep 26 '23 at 16:48

DEEPANWITA Roy

2

https://oeis.org/A001923 – JMoravitz Sep 26 '23 at 16:58
...in other words, as OEIS does not have a closed form, it is highly unlikely that a closed form of this sum is known. – Theo Bendit Sep 26 '23 at 17:08
about summing the reciprocals https://mathworld.wolfram.com/SophomoresDream.html – Will Jagy Sep 26 '23 at 17:52
Does this answer your question? Closed form of sum of n^n series? – Dietrich Burde Sep 26 '23 at 18:16

How to find the summation of the above series upto $n$ terms?

0 Answers0