Now a property of this is that the angle between the tangent at any point B and the line joining origin to B is constant . My question is why does this happening? I was able to prove this but don't understand why this happens.
1 Answers
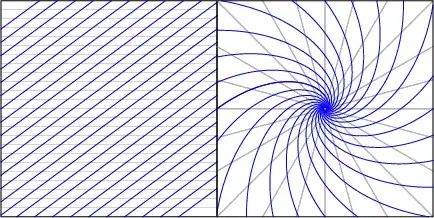
Let's start with a seemingly-unrelated question. Introduce Cartesian coordinates $(u, v)$ in the Euclidean plane, and consider the set of all horizontal lines.
Question: Which curves meet all horizontal lines at the same angle?
Every non-horizontal line meets each horizontal line at the same angle. The angle is determined by the slope: The line $u = kv + u_{0}$ meets each line $v = v_{0}$ at angle $\phi$ satisfying $\cot\phi = k$.
Now, the magic: Consider the mapping $(u, v) \mapsto (x, y)$ defined by \begin{align*} x &= e^{u} \cos v, \\ y &= e^{u} \sin v. \end{align*} In complex terms, if we write $w = u + iv$ and $z = x + iy$, this is the exponential mapping $z = \exp(w)$: Euler's formula $e^{i\theta} = \cos\theta + i\sin\theta$ allows us to write \begin{align*} z = x + iy &= e^{u} \cos v + ie^{u} \sin v \\ &= e^{u}(\cos v + i\sin v) \\ &= e^{u} \cdot e^{iv} = e^{u + iv} = \exp(w). \end{align*} This mapping $\exp$ satisfies three properties that answer your question:
- $\exp$ maps the plane to the plane with the origin removed in an angle-preserving way. (This is a feature of all complex-differentiable mappings with no critical points.)
- $\exp$ maps horizontal lines $v = v_{0}$ to rays $\theta = v_{0}$ from the origin.
- $\exp$ maps diagonal lines $u = kv + u_{0}$ to logarithmic spirals.
Since every line meets all horizontal lines at a constant angle, every logarithmic spiral meets all rays from the origin at a constant angle.
To see $\exp$ preserves angles, we can calculate the derivative matrix $$ d\exp(u, v) = \left[\begin{array}{@{}rr@{}} e^{u}\cos v & -e^{u}\sin v \\ e^{u}\sin v & e^{u}\cos v \\ \end{array}\right] = e^{u} \left[\begin{array}{@{}rr@{}} \cos v & -\sin v \\ \sin v & \cos v \\ \end{array}\right]. $$ At each point this is the composition of rotation and scaling, so at each point the derivative preserves angles.
To see that lines map to logarithmic spirals, we can parametrize the line $u = kv + u_{0}$ by taking $v = t$ and $u = kt + u_{0}$, i.e., $(kt + u_{0}, t)$. Applying $\exp$ to this gives a parametric description of the image curves: $$ \gamma(t) = \exp(kt + u_{0}, t) = e^{kt + u_{0}}(\cos t, \sin t), $$ or \begin{align*} x &= e^{kt + u_{0}} \cos t, \\ y &= e^{kt + u_{0}} \sin t. \end{align*} This curve traces the polar graph $r = e^{k\theta + u_{0}}$, a logarithmic spiral. To check formally that these are your curves, note that
- $y/x = \sin\theta/\cos\theta = \tan\theta$, and
- $\ln r = k\theta + u_{0}$, or $\theta = \frac{1}{k} (\ln r - u_{0}) = \frac{1}{2k} \bigl(\ln(x^{2} + y^{2}) - 2u_{0}\bigr)$. (The formula in your Desmos window has $u_{0} = 0$ and $k = 1/2$, but the plot shows multiple spirals, which correspond to different values of $u_{0}$. By contrast, changing $k$ changes the "slope" of the spirals, as in the animation loop above.)
- 78,195
-
Wow! i am truly impressed. I was never introduced to math like this. Could you explain what does mapping entirely mean? – TheCuriousOne Sep 23 '23 at 16:29
-
A mapping in the sense of mathematics is a generalization of a mathematical function in the sense of calculus, whose inputs and outputs might be points in the plane, or a higher-dimensional space, or more general sets. The name comes from cartography, which maps parts of the earth's surface to flat sheets of paper. A complete answer would be lengthy, but that may give some useful search terms? – Andrew D. Hwang Sep 23 '23 at 17:17
-
could you provide some basic reading materials? – TheCuriousOne Sep 23 '23 at 18:31
-
Depending on your background and interests, Wikipedia's list of map projections might be as good a starting place as any. Math students tend to pick up this material in bits and pieces, starting with formalities often seen in multivariable calculus. In my experience there's not a standard course or textbook specifically devoted to mappings. – Andrew D. Hwang Sep 23 '23 at 21:13
-
I am currently a student in high school. What be a good starting point? – TheCuriousOne Sep 24 '23 at 02:47
-
Polar coordinates in precalculus and calculus used to be a standard entry point, but in my experience have fallen from the curriculum. That may be how you came to look at these spirals? Whether or not, older analytic geometry and (pre-)calculus textbooks should be good places to read more. At the university level, linear algebra, multivariable calculus, differential geometry, and complex analysis are standard places to pick up tools and examples. – Andrew D. Hwang Sep 24 '23 at 21:12
-
I actually came across doing calculus itself. Could you recommend some books for my level. Also I study an Indian curriculum. – TheCuriousOne Sep 25 '23 at 01:59
-
I don't have a recommendation offhand, I'm afraid. In the US there used to be dozens of books, and I don't recall the name or authors of the one when I was a student. A search of the Internet Archive turned up this Russian textbook (translated to English) that I have not read, but looks sort of promising: https://archive.org/details/vygodsky-mathematical-handbook-higher-mathematics-mir/mode/2up <> Do you have a teacher you can ask? – Andrew D. Hwang Sep 27 '23 at 18:36
-
D Hwang No.......... – TheCuriousOne Sep 28 '23 at 02:28