if $x^y =y^x$ then what is all possible solution on $\mathbb{C}$
I was playing with graphing calculator and tried the equation $x^y =y^x$ and I was expecting another set of solution other that the trivial solution $x=y$ because $2^4 =4^2 $ and when I graphed the equation I got 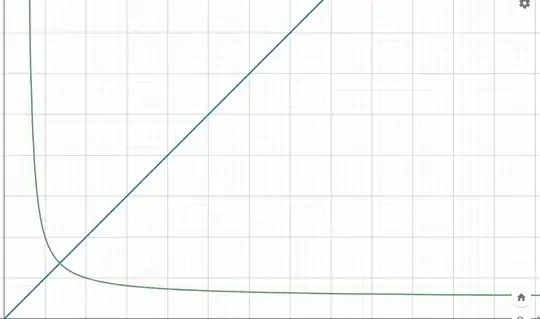
but I have no Idea what is the formula of the green curve I could just proof that the intersection between the $x=y$ and the other set of solutions is $(e,e)$ because $e^a >a^e$ and I am curious if there is another set of solutions on $\mathbb{C}$ ( I don't know how to graph complex function and i don't know if it is even possible to graph function of several complex variables also I haven't study complex analysis yet )