Is $X Y/|Y|$, where $X, Y \text{ i.i.d. } \sim N(0, 1)$, normally distributed?

Question

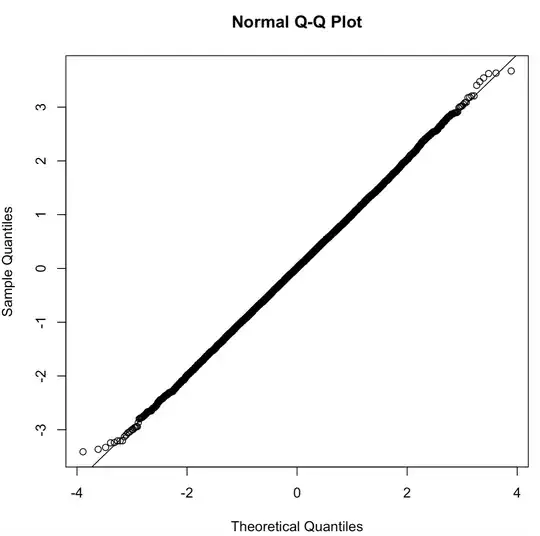
In this answer, it was shown that the product of two i.i.d. standard normal r.v.s is not normally distributed. What if we scale one of them? In other words, if $X, Y \text{ i.i.d } \sim N(0, 1)$, what is the distribution of $Z := X\frac{Y}{|Y|}$? By looking at he distribution function of $Z$ (though I didn't finish the calculation), $Z$ is unlikely to be normal. However, the simulation seems to suggest that $Z$ is normal (the QQ plot of $10,000$ realizations of $Z$ is shown below). Is there a clever way to prove or disprove $Z$ is normally distributed?

Answer 1

Conditional on $Y = y$, $Z$ is $\mathcal N(0,1)$. Since the regular conditional distribution of $Z$ is the same for all $y$, we conclude $Z$ is independent of $Y$. In particular, $Z\sim \mathcal N(0,1)$.

Generalizing, if $X\sim \mathcal N(\mu,\sigma^2_1),Y\sim \mathcal N(0,\sigma^2_2)$ one still has $Z\sim \mathcal N(0,\sigma_1^2)$. It is easy to see that this fails if $E(Y)\neq 0$.