How can I (algebraically) prove that the relation $x^3+y^3-12xy=0$ has two tangents at the origin?

Question

How can I (algebraically) prove that the relation $x^3+y^3-12xy=0$ has two tangents at the origin?

Answer 1

A plane algebraic curve is defined by a polynomial in two variables $f(x, y)$, where $f(x, y) = 0$.

To show that something happens at the origin, we first need to verify that the origin is on the curve. The origin is $(x, y) = (0, 0)$, so we plug $x = y = 0$ into $f$. Do we get 0? Good. The origin $(0, 0)$ is on $C$.

The next thing to do is determine if the curve is singular at $(0, 0)$. Most points on most curves are smooth, and there is a single tangent at smooth points. At singular points, there could be all kinds of different behaviors.

The test for smoothness is simple: compute the gradient of $f$. The gradient is just the vector $\nabla f = (\partial f / \partial x, \partial f / \partial y)$, evaluated at the point of interest. If the gradient is nonzero, there is a tangent: the line perpendicular to the gradient. If the gradient vanishes, we have a singularity.

In our case, $\nabla f = (3x^2 - 12y, 3y^2 - 12x)$, and indeed $\nabla f = (0, 0)$ at $(0, 0)$. So we already know that $C$ is singular at $(0, 0)$, but we still need to determine the type of singularity. Are there two tangents there? None? Many?

These are some of the ways a (real) plane algebraic curve can be singular at the origin:

(The top left example is actually the present curve).

To find the different tangents, we can write $x=at$ and $y=bt$. This describes a straight line through the origin as $t$ varies, and it's a bit better than writing $y=ax$ because then we would miss the vertical line.

Putting $(x,y)=(at,bt)$ in the equation we get

$(at)^3+(bt)^3-12(at)(bt)=0$

or

$t^2(a^3t+b^3t-12ab)=0$

First of all, no matter what $a$ and $b$ are (i.e. no matter what line we are thinking of), we see that $t=0$ is a double root of this equation, which means that every straight line through the origin meets our curve twice at the origin.

But, when $a=0$ or $b=0$ (but not both), the term $-12ab$ disappears and we get $t^3(a^3+b^3)=0$, and now $t=0$ is a triple root. That means that the lines $(x=t,y=0)$ and $(x=0,y=t)$ meet our curve not twice (as usual) but three times – and that extra multiplicity is, geometrically, a tangency. Instead of slicing right through, the line gently hugs the curve, touching it one extra time.

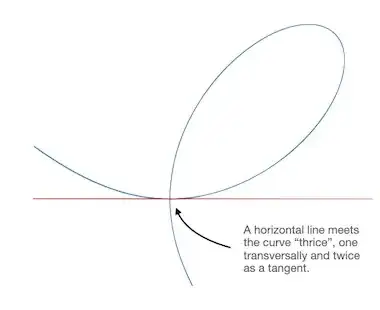
It's beautiful to see how an algebraic property (the degree $k$ of the factor $t^k$) faithfully captures the geometry.

Answer 2

There is a very simple technique using the so-called Newton's polygon associated with the given polynomial in two variables :

The idea is first to associate the point $(n,p) \in \mathbb{N}^2$ to each monomial $ax^ny^p$ (coefficient $a$ isn't taken into account). For example, to the polynomial equation $13x^3y^2-5x^2y^2+5xy+7x=0$, the following points will be associated $(3,2), \ (2,2), \ (1,1), \ (1,0)$. In a second step, the convex hull is considered, and, for our purpose (being able to have all branches passing through the origin) considering only the lower part of the convex envelope as in the following example borrowed to this site. We see the behavior of the curve given by equation $-x^4+x^2y^3+\cdots = 0$ in the vicinity of the origin. On the right graphic, one sees two branches : one of them looks parabolic (think to $y=ax^2$), the other one looks "pinched", reminding, with a little habit, a local behavior of the form $y=ax^{p/q}$ (fractional exponent).

Now, the Newton polygonal is going to confirm our intuition.

Indee, the lower part of the convex hull is constituted by two line segments :

• The first one joining $(0,4)$ to $(2,1)$ with slope $\color{red}{2/3}$ when looking the line at $90°$.

• The second one joining $(2,1)$ to $(4,0)$ with slope $\color{red}{2}$.

These 2 slope values give the exponents we are looking for :

$$y=x^{\color{red}{2/3}} \ \text{in the first case and } \ y=x^{\color{red}{2}} \ \text{in the second case}$$

Moreover, there are exactly two different branches passing through the origin, therefore two tangents.

Up to you : check that it works on your polynomial !

I will not do any theory justifying this technique. You will find it, together with other uses of Newton's polygon for example on this site in certain questions/answers like this one.

Answer 3

Your derivative computation is wrong. Also, you cannot use these formulas here, as at the origin, there are multiple tangents. Given a polynomial function $f(x,y)$, one can write it as a sum of forms, say $f(x,y)=f_0+f_1+\cdots+f_m$, where $m$ is the total degree of $f$ and $f_i's$ are either zero or is a form in $x,y$ having total degree $i$, for each $0\le i\le m$. The tangent(s) at the origin will be given by setting $f_k=0$ and factorizing it into linear forms (at least over $\mathbb{C}$), where $k$ is the least index $i$ such that $f_i$ is not zero. In your case, $f_k=-12xy$ and so the tangents at the origin are $x=0,y=0$.

Answer 4

It does look like $x y = 0$ in a neighborhood of $(0,0)$.

Let's try to show that the function factorizes as a product in a neighborhood of $(0,0)$. Apply a linear change of coordinates

$$(x,y) = (p+q, p-q)$$ and get

$$p^2 - q^2 - \frac{p^3}{6} - \frac{p q^2}{2}=0$$

or

$$p^2(1 -\frac{p}{6}) = q^2( 1 + \frac{p}{2})$$

that is

$$q = \pm \sqrt{\frac{1-\frac{p}{6}}{1 + \frac{p}{2}}}\cdot p$$

Now we see that around $(0,0)$ ( for $|p|$ small) the curve is the union of the graphs of two functions.

---

Note: if we had a curve of the form

$$F(p,q) = p^2 - q^2 + \textrm{ higher order terms} = 0$$ then each of the higher order terms is divisible by $p^2$ or $q^2$ ( or both), so we can group as

$$p^2 ( 1 + \textrm{h.o.t}) - q^2( 1 + \textrm{h.o.t}) = 0$$ or $$p_1^2 - q_1^2 =0$$ where $$p_1 = p \sqrt{ 1 + \textrm{h.o.t}} \\ q_1 = q \sqrt{1 + \textrm{h.o.t}}$$

Now $(p_1, q_1)$ is a new system of coordinates around $(0,0)$, so the curve around $(0,0)$ is the union of two curves $q_1 = \pm p_1$.

This is a particular case of Morse lemma.

$\bf{Added:}$ We can try some ad-hoc methods on curves of the form

$$F(x,y) = x^3 - y^3 + \textrm{h.o.t}=0$$

around $(0,0)$. Now the higher order terms are of degree $\ge 0$, so they either are divisible by $x^3$ or $y^3$, or are $ c x^2 y^2$. Multiply $F$ by $1-c x^2 y^2$ to get an equivalent equation around $(0,0)$ that now has all terms divisible by $x^3$ or $y^3$

$$x^3(1+ \textrm{h.o.t}) - y^3( 1+ \textrm{h.o.t.})= 0$$

or $$x_1^3 - y_1^3= 0$$

The factor $x_1^2 + x_1 y_1 + y_1^2 = 0$ gives only $(0,0)$, so the real curves appears to be the smooth $x_1 - y_1 = 0$.