A generalization of Pythagoras'

Question

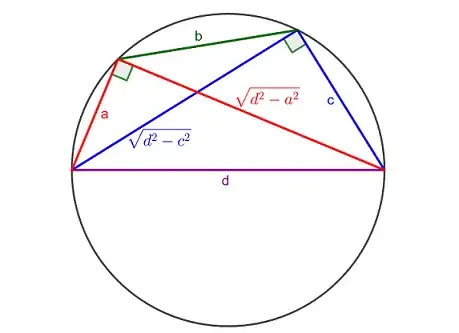
Consider a quadrilateral inscribed in a semicircle of diameter $d$, as in the picture below, then $$d^2 = a^2 + b^2 + c^2 + \frac{2 a b c}{d}$$

Notes:

1. If one of the $a$, $b$, $c$ equals $0$, we get Pythagoras'

2. An older problem on this site asks (essentially) to determine $d$ if $(a,b,c) = (2,7,11)$.

3. The set $\{ (a,b,c,d) \ | d^3 = (a^2 + b^2 + c^2)d + 2 a b c\}$ can be parametrized by \begin{eqnarray} a &=& p(-p^2 + q^2 + r^2)\\ b&=&q(p^2 - q^2 + r^2)\\ c&=& r(p^2 + q^2 - r^2)\\ d&=& 2 p q r \end{eqnarray}

4. Provided as reference.

Any feedback would be appreciated!

$\bf{Added:}$

1. will write an answer tomorrow, perhaps some users would like to solve it on their own.

2. In the answer of @Cristhian Camacho to the older problem linked, we find this formula.

$\bf{Added:}$

A possible solution : the relation is equivalent to

$$1 = x^2 + y^2 + z^2 + 2 x y z$$ where $x = \frac{a}{d}, \ldots$, but then also $x = \sin \frac{\alpha}{2}, \ldots$, with $\alpha+ \beta + \gamma = \pi$. Now we have to show that if $u + v+w = \frac{\pi}{2}$, then

$$ 1- (\sin^2 u + \sin^2 v + \sin^2 w) - 2 \sin u \sin v \sin w$$ In fact we have a factoring.

Equivalently, one can show that if $\phi+ \psi + \theta = \pi$ ( angles of a triangle) then

$$1 = \cos^2 \phi + \cos^2 \psi + \cos^2 \theta + 2 \cos \phi \cos \psi \cos \theta$$

( $\phi = \frac{\pi}{2} - \frac{\alpha}{2}, \ldots$). This also provides the parametrization of the set, using formulas for the $\cos$ in a triangle.

$\bf{Added:}$ Just an idea how to handle more general things: say we want to determine a relation between the cosines of some angles with a sum a given rational multiple of $\pi$. Write $x_i = \cos \phi_i$, with $\sum \phi_i = \frac{ k \pi}{l}$. Then $\cos \phi_i = \frac{1}{2}( t_i + \frac{1}{t_i})$ and $(t_1 \cdots t_n)^l = (-1)^k$. Eliminating $t_i$ from the above gets a relation between the $x_i$. It could be rather involved, but our case is simple( $\phi_1 + \phi_2 + \phi_3 = \pi$, so $t_1 t_2 t_3 + 1 = 0$, and we get $1 = x_1^2 + x_2^2 + x_3^2 + 2 x_1 x_2 x_3$).

Answer 1

Clearly, due to $90^\circ$ subtended by the diameter on the semicircle, the diagonals are $\sqrt{d^2-a^2}$ and $\sqrt{d^2-c^2}$. By Ptolemy theorem, which says that product of diagonals of a cyclic quadrilateral equals the sum of products of opposite sides, we have $$\sqrt{d^2-a^2}\cdot\sqrt{d^2-c^2}=ac+bd$$ On squaring and simplifying, this rearranges into $$d^2=a^2+b^2+c^2+\frac{2abc}{d}$$

Answer 2

As shown in the figure below, I've added lines joining the $2$ points on the upper part of the circle to the center (labeled $O$), and labeled the points around the circle, starting from the left and going clockwise, as $A$, $B$, $C$ and $D$.

With $r$ being the circle's radius, we have

$$\lvert AO\rvert = \lvert BO\rvert = \lvert CO\rvert = \lvert DO\rvert = r \tag{1}\label{eq1A}$$

Also, label the angles in the the upper semi-circle around the point $O$ as

$$\measuredangle AOB = \alpha, \; \measuredangle BOC = \beta, \; \measuredangle COD = \gamma, \;\;\; \alpha + \beta + \gamma = \pi \tag{2}\label{eq2A}$$

Next, using the law of cosines on $\triangle AOB$, $\triangle BOC$ and $\triangle COD$ gives

$$a^2 = r^2 + r^2 - 2r^2\cos\alpha = 2r^2(1 - \cos\alpha) = \frac{d^2}{2}(1 - \cos\alpha) \tag{3}\label{eq3A}$$

$$b^2 = r^2 + r^2 - 2r^2\cos\beta = 2r^2(1 - \cos\beta) = \frac{d^2}{2}(1 - \cos\beta) \tag{4}\label{eq4A}$$

$$c^2 = r^2 + r^2 - 2r^2\cos\gamma = 2r^2(1 - \cos\gamma) = \frac{d^2}{2}(1 - \cos\gamma) \tag{5}\label{eq5A}$$

Adding the above $3$ equations together results in

$$a^2 + b^2 + c^2 = \frac{d^2}{2}(3 - (\cos\alpha + \cos\beta + \cos\gamma)) \tag{6}\label{eq6A}$$

As shown in Prove trigonometry identity for $\cos A+\cos B+\cos C$, we have

$$\cos\alpha + \cos\beta + \cos\gamma = 1 + 4\sin\left(\frac{\alpha}{2}\right)\sin\left(\frac{\beta}{2}\right)\sin\left(\frac{\gamma}{2}\right) \tag{7}\label{eq7A}$$

By drawing perpendicular bisector lines from $O$ to each of $AB$, $BC$ and $CD$, we see that

$$\sin\left(\frac{\alpha}{2}\right) = \frac{\left(\frac{a}{2}\right)}{r} = \frac{\left(\frac{a}{2}\right)}{\left(\frac{d}{2}\right)} = \frac{a}{d} \tag{8}\label{eq8A}$$

Similarly, $\sin\left(\frac{\beta}{2}\right) = \frac{b}{d}$ and $\sin\left(\frac{\gamma}{2}\right) = \frac{c}{d}$. Substituting these into \eqref{eq7A}, and then that result into \eqref{eq6A}, gives

$$\begin{equation}\begin{aligned} a^2 + b^2 + c^2 & = \frac{d^2}{2}\left(3 - 1 - \frac{4abc}{d^3}\right) \\ a^2 + b^2 + c^2 & = d^2 - \frac{2abc}{d} \\ d^2 & = a^2 + b^2 + c^2 + \frac{2abc}{d} \end{aligned}\end{equation}\tag{9}\label{eq9A}$$

Answer 3

In the figure,

$$x=y$$ $$\because \sin y = \frac{c}{d}$$ $$\therefore \sin x = \frac{c}{d} $$

Using Cosine Rule on $\Delta ABC$,

\begin{align} AC^2 &= a^2+b^2-2ab\cos(90^{\text {o}}+x) \\ &= a^2+b^2+2ab\sin x \\ &= a^2+b^2+2ab\left(\frac{c}{d} \right) \\ &= a^2+b^2+\frac{2abc}{d} \end{align}

In $\Delta ACD$, $$AD^2 = CD^2+AC^2$$ $$d^2=c^2+a^2+b^2+\frac{2abc}{d}$$