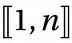Conventional set notation for integers between m,n CS Theory/Math literature

Question

This is a pretty simple, straightforward question. I've seen in the literature $[n]=\{0,1,2,\dots,n-1\}$ and $[n]=\{1,2,3,\dots,n\}$. Is there a similar convention for $[n]\backslash[m]=\{n,n+1,\dots,m\}$? Maybe [n,m] or something?

I can't seem to find a resource on the net that compiles conventions. If you happen to have a list of conventions or an answer, I'd appreciate it. I'm trying to save valuable space and don't want to confuse a reader with an unexpected definition.

Some of these responses were a bit helpful: About Math notation: the set of the $n^{th}$ natural numbers

Answer 1

For $n \le m$, $[n]\subset[m]$ so $[n]\cap[m]=[n]$. Whereas the set you want is $\{n, n+1,\dots,m\}=[m]\setminus [n]$. And I've seen the notation $⟦n,m⟧$. It is possible to make thos with \llbracket or other commands but they all require additional packages, none of which seem to be available here.

Answer 2

"Concrete Mathematics" by Graham, Knuth and Patashnik uses $[a \, .. b]$ for $\{a, a+1, a+2, \dots , b\}$ and $[a \, .. b)$ for $\{a, a+1, a+2, \dots , b-1\}$ .

Answer 3

In France, students are taught to use the notation

to mean $\{1,2,\dots,n\}$. We can use the notation for $\{m,\dots,n\}$.

It is not listed in the ISO 80000-2, which is an international standard that defines mathematical signs and symbols.

To use it in LaTeX:

FYI: Why is American and French notation different for open intervals (x, y) vs. ]x, y[?