Evaluation of $\int_{-\infty}^{\infty} \frac{\sin ^m(x)}{x^n} d x$ without contour integration.

Question

The integral $$\int_{-\infty}^{\infty} \frac{\sin ^m(x)}{x^n} d x$$ is a very important result. The cases for $m=n=1$ is well known. I tried generalizing it for $m,n$ and I came across a lot of references which used contour integration. My question is whether the given integral can be evaluated without contour integration. A much more challenging question would be to evaluate the integral for $m, n \in \mathbb{R}$ or even better, $m, n \in \mathbb{C}$. Thank you

Answer 1

Here's a proof, using Fourier analysis, that for $m=n\in\mathbb N$,

$$\boxed{\int_{-\infty}^{\infty} \frac{\sin ^n(x)}{x^n} dx = \frac{\pi}{2^n (n-1)!}\sum_{k=0}^n {n \choose k} (-1)^k (n -2k)^{n-1} \text{sgn}(n -2k)}$$

Here is a Desmos link and some of the first few values: \begin{array}{|c|c|c|c|c|c|} \hline n & 1 & 2 & 3 & 4 & 5 & 6\\ \hline I_n & \pi & \pi & \frac{3\pi}4 &\frac{2\pi}3&\frac{115\pi}{192}&\frac{11\pi}{20}\\ \hline \end{array}

Now onto the proof. We take the following convention for the Fourier transform of a function $f\in\mathbb L^1(\mathbb R)$: $$\widehat f(\omega) = \int_{\mathbb R} e^{-i \omega x}f(x)dx$$ Let $f_n(x)=\left(\frac{\sin x}x\right)^n$. Then, based on the definition above, the integral we need to compute is $\widehat {f_n}(0)$.

We're going to compute the general formula for $\widehat {f_n}(\omega)$. Note: Those Fourier transforms are known as box splines and are important in numerical analysis and interpolation. This is what they look like:

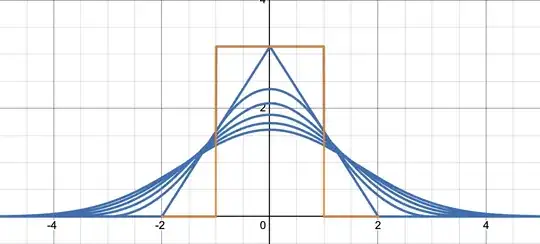
Lemma: For $n\geq 1$, $$\widehat{f_n}(\omega)=\frac{\pi}{2^n (n-1)!}\sum_{k=0}^n {n \choose k} (-1)^k (\omega +n -2k)^{n-1} \text{sgn}(\omega +n -2k)$$ Proof: We proceed by induction.

For $n=1$, the formula reduces to $\pi$ times the indicator function of $[-1, 1]$, and you can verify that its inverse Fourier transform is $f_1$.

Suppose the formula is valid for some $n\geq 1$. Then, note that $f_{n+1}=f_1 f_{n}$. Thus, since the Fourier transform maps products to convolutions, we have $\widehat{f_{n+1}} = \frac 1 {2\pi} \cdot \widehat{f_1} \ast \widehat{f_n}$. This implies that $$\frac{d\widehat{f_{n+1}}}{d\omega} = \frac{d\widehat{f_{1}}}{d\omega} \ast \widehat{f_n} = \frac 1 2 \cdot (\delta_{-1} - \delta_{1}) \ast \widehat{f_n}$$ In other words, $$\frac{d\widehat{f_{n+1}}}{d\omega}=\frac{\widehat{f_n}(\omega+1)-\widehat{f_n}(\omega-1)}2$$ Thus, defining $g_n(x)=x^{n-1}\text{sgn}(x)$, $$\begin{split} \frac{d\widehat{f_{n+1}}}{d\omega} &= \frac 1 2 \cdot \frac{\pi}{2^n (n-1)!}\sum_{k=0}^n{n\choose k}(-1)^k g_n(\omega+n+1-2k)\\ &- \frac 1 2 \cdot \frac{\pi}{2^n (n-1)!}\sum_{k=0}^n{n\choose k}(-1)^k g_n(\omega+n+1-2k-2)\\ &=\frac 1 2 \cdot \frac{\pi}{2^n (n-1)!}\sum_{k=0}^n{n\choose k}(-1)^k g_n(\omega+n+1-2k)\\ &- \frac 1 2 \cdot \frac{\pi}{2^n (n-1)!}\sum_{k=1}^{n+1}{n\choose k-1}(-1)^{k+1} g_n(\omega+n+1-2k)\\ &= \frac 1 2 \cdot \frac{\pi}{2^n (n-1)!} \left[g_n(\omega +n+1) +(-1)^{n+1} g_n(\omega-n-1) +\\ \sum_{k=1}^{n}(-1)^k\left( {n\choose k} + {n\choose k-1}\right)g_n(\omega+n+1-2k)\right]\\ &= \frac 1 2 \cdot \frac{\pi}{2^n (n-1)!}\sum_{k=0}^{n+1}{n+1\choose k}(-1)^k g_n(\omega+n+1-2k) \end{split}$$ To prove the formula, we only need to integrate w.r.t. $\omega$, and use the fact that a primitive of $g_n(\omega)$ is $\frac {g_{n+1}(\omega)}n$. Note that the integration constant is $0$ as we expect the limit of $\widehat {f_{n+1}}$ at infinity to be zero (because it is the repeated convolution of $\widehat {f_1}$, which has a compact support).

$$\widehat{f_{n+1}}(\omega) = \frac 1 2 \cdot \frac{\pi}{2^n (n-1)!}\cdot \frac 1 n \sum_{k=0}^{n+1}{n+1\choose k}(-1)^k g_{n+1}(\omega+n+1-2k)$$

This concludes the proof of the lemma. To obtain the value of the integral, all that's left to do is to evaluate at $\omega=0$.