Does the word "if" have a different meaning in mathematical writing than in everyday English?

Question

In a recent answer to a question about material implication and vacuous truths, I wrote:

The word "if" has two different meanings. The meaning that's used in mathematical writing is different from the meaning that's used in everyday English.

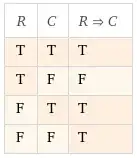
In mathematical writing, the phrase "if X, then Y" is defined as meaning "either not-X, or Y." Whenever this definition conflicts with the everyday meaning of the word "if," we disregard the everyday meaning and use this definition instead.

However, I was a little surprised to receive a comment stating, "I strongly disagree with the first paragraph of this answer" (which is the first paragraph quoted above.) Judging by the number of upvotes I see on the comment, there are at least three people who disagree with me on this point, so now I'm wondering if I was mistaken in my original claim.

My current belief is that in mathematical writing, the word "if" denotes material implication, but in everyday English, it does not. Am I right about that? If not, which part am I wrong about and why?

(Note that I'm not claiming that the idea of material implication is wrong in any way; what I am claiming is that material implication and the everyday meaning of the word "if" are not identical to each other.)

---

For what it's worth, I find the following thought experiment to be a convincing argument that in everyday English, the word "if" does not refer to material implication.

In the fictional land of Fictionlandia, a notorious con artist named Ruth Roe sets up a stand selling elixirs. She makes all sorts of promises about her elixirs to passersby: "If you drink this, your hair will grow back tomorrow!" "If you drink this, your cataracts will clear up instantly!" "If you drink this, you will be immune to all types of poison forevermore!" However, nobody ever buys any of the elixirs, and at the end of each day, Ruth pours them all out in the street.

Eventually, one Jennifer Doe has had enough, and takes Ruth to court for false advertising. In her own defense, Ruth argues that every statement she made was completely true. After all, nobody ever drank the elixir! Since the antecedent of each of her claims (namely, "you drink this") turned out to be false, that means that each of her claims was a 100% true statement.

Jennifer says that Ruth's argument is nonsense, and that if some liquid has no cataract-healing properties, then the statement "If you drink this, your cataracts will clear up instantly" is false regardless of whether or not anyone actually drinks the liquid.

I think (but I'm not certain) that most of us would agree with Jennifer's argument, not Ruth's.

Answer 1

You are right, and in fact there's an entire Wikipedia article about this phenomenon called paradoxes of material implication. If that's not authoritative enough you can also consult the Stanford Encyclopedia of Philosophy's page on the logic of conditionals, which begins:

Logics of conditionals deal with inferences involving sentences of the form “if A, (then) B” of natural language. Despite the overwhelming presence of such sentences in everyday discourse and reasoning, there is surprisingly little agreement about what the right logic of conditionals might be [emphasis mine], or even about whether a unified theory can be given for all kinds of conditionals. The problem is not new, but can be traced back to debates between Megarian and Stoic logicians (see Sextus Empiricus, Outlines of Scepticism II, 110–112; Kneale & Kneale 1962; Sanford 1989; Weiss 2019).

Personally I think it's fair to assert that the ordinary everyday use of "if" carries an implication of meaningful causality between the antecedent and the consequent; some of the paradoxes of material implication (including the one you point out) have to do with situations where the antecedent and the consequent have nothing meaningful to do with each other but where the antecedent is technically false and so forth. I think it's also fair to assert that the ordinary everyday use of "if" involves counterfactual reasoning in a way that the ordinary mathematical "if" does not support; this is modeled to some extent by the strict conditional in modal logic.

Answer 2

Here's a story about the mathematical and the ordinary language use of "if" (or at least the ordinary use of non-subjunctive conditionals).

Start by considering the relation between A but B and A and B. It is very plausible to suggest that these two claims don’t differ in what it takes for them to be true. Rather, the contrast between ‘but’ and the colourless ‘and’ is (very roughly) that A but B is typically reserved for use when the speaker presumes that there is some kind of contrast between the truth or the current relevance of A and of B. If we regiment a passage of reasoning which uses but using the truth-functional $\land$, we miss out that indication of speaker-attitude, but arguably don't miss out something relevant to the assessment of the reasoning as far as its logical validity (truth-preservation) is concerned.

Well, could it be similar for a pair of claims for the form if A then C and the truth-functional A → C? Perhaps again these two don’t differ in what it takes for them to be true. But still, there is a difference between ‘if’ and the colourless material conditional. For if A then C is reserved for use when the speaker is – as it were – promising to endorse a modus ponens inference to the conclusion C should it turn out that A is true.

This seems a friendly amendment of the bald equation of 'if' with '→. For it keeps the core idea that the assertions if A then C and A → C (i.e. not-A or C) come to the same as far as their logic-relevant truth conditions are concerned. But we also get an explanation for why (for example) the inferential move from not-A to if A then C typically seems quite unacceptable (even though truth-preserving).

How so? The plausible suggestion is that the use of ‘if’ signals that the conditional it expresses can be used in an inference to its consequent. Now, suppose that I start off by believing not-A. Then, I will accept not-A or C or equivalently A → C. But of course, I won’t in this case be prepared to go on to infer C should I later come round to accepting A. Instead, because I have changed my mind about the truth value of A, I will now take back my earlier endorsement of A → C. In other words, if my only reason for accepting A → C is a belief in not-A, I won’t be prepared to go on to endorse using the conditional in a modus ponens inference to the conclusion C. And that is why, according to this suggestion about the role of ‘if’, I won’t be prepared to assert if A then C just on the ground that not-A.

Which is the beginning of a neat and attractive story. If it is right, then we can regiment simple conditionals using the arrow, confident that informal conditional claims and their formal regimentations can match at least on their core truth-relevant aspects of meaning, which is what logic cares about. And is what mathematical reasoning cares about. We don't have to say that "if" means just the same as "→" (any more than we say that "but" means just the same as "$\land$"). But perhaps we can say that the core truth-relevant meaning of "if" is captured by "→".

Now, I'm not hereby trying to sell this particular story! But it does illustrate how it might be possible to (as it were) have our cake and eat it -- i.e. acknowledge that in a broad sense of meaning "if" doesn't straightforwardly mean the same as the material conditional, while also allowing that the material conditional gets the core truth-relevant content right so is apt of logical/mathematical purposes.

Answer 3

The claim

If you drink the elixir, your hair will grow back.

arguably means more formally:

In all possible timelines in which you drink the elixir, your hair grows back.

which is equivalent to

For all possible timelines $t$, if you drink the elixir in timeline $t$, then your hair grows back in timeline $t$.

In this last sentence, the "if...then" is a material conditional, but not drinking the elixir in one timeline doesn't make the claim true.

I've never seen a "non-material implication" example that couldn't be regarded as just an implicit forall around a material implication.

Answer 4

I think we agree with Jennifer that Ruth's claim is rubbish, regardless of whether we are reading it colloquially (1) or mathematically (2). Explicating each case:

1. Drinking Ruth's elixir causes cataracts to instantly clear up.

2. At any time, any person who drinks Ruth's elixir instantly has their cataracts cleared up. $\quad\forall t\;\forall p\,\Big(E(p,t)\implies C(p,t)\Big)$

   The fact that nobody has ever (till now) drank the elixir is not sufficient evidence that Ruth's claim is (vacuously) true.

The word "if" has two different meanings. The meaning that's used in mathematical writing is different from the meaning that's used in everyday English.

I think it’s more accurate to say that ‘if’ has more possible meanings in everyday usage than just the mathematical one, which the material conditional underpins.

Answer 5

Ressource : Modal logic's solution and Pragmatics' solution to the paradoxes of material implication https://canvas.eee.uci.edu/courses/3605/files/1512625/download?verifier=heyAvjPaRvYoB18WKUPaVbCHFVoFgHMZesSR3vcA

---

Short answer : same semantics, different pragmatics

---

In everyday language, utterances get a meaning from the pragmatic aspect of language ( that is, its relation to its users and to the situation in which sentences are pronounced).

Note: This aspect of language has been theorized by Paul Grice in his paper "Logic and conversation".

If a father says to his son :

' If you get good grades this year, I'll offer you a trip to Disney World"

the father has implicated that if his son does not get good grades, he will not offer the trip. Why? Because in case the father intends to offer the trip whatever the grades may be, he has not played " fairly" the conversational game , which tacitly requires that one provides the maximal amount of information he has got in his possession.

So, the semantics of the " if ... then" connective is the same as in mathematics , but the pragmatics is different, and , due to pragmatics, the " if ... then" implicates an " if and only if".

In the same way, suppose that you ask a person whether she lives in New York, and the persons answers: " I live in the USA" ; you would not say that the person uses the expression in a way that deviates from its standard meaning; rather you would infer that the person implicates you're too curious.

Answer 6

For me the everyday use of if can be given by the table below

proposition X    proposition Y    possible by if statement
true             true             yes
true             false            no
false            true             undetermined
false            false            undetermined 

The second row which is excluded by the if statement can be seen as defining the if statement and it is equivalent to

$$\lnot(X \land \lnot Y)$$

and also

$$\lnot X \lor Y$$

These do not have different meanings but are just the same thing expressed in different ways.

---

The discussion between Jennifer and Ruth doesn't seem to be about the meaning of an if statement, but more like whether a claim of a vacuous truth can be made when advertising the effect of a non-functional elixir.

The antecedent "If you drink this..." may not happen in reality, but we can imagine a hypothetical world where it is true.

Answer 7

Does the word "if" have a different meaning in mathematical writing than in everyday English?

In daily discourse, "if" is often mistakenly used to indicate causal relationships.

EDIT

Apart from supposed causal relationships, the meaning of "if" in daily discourse is subsumed by the mathematical meaning. Some features of the mathematical meaning are simply not commonly used in daily discourse.

EXAMPLE

Perhaps an example will clear things up. Consider the sentence "If it is raining ($R$), then it is cloudy ($C$)." Symbolically, we can write:

$~~~~~R \implies C$

This does not mean that rain causes cloudiness. It means only that it is not the case that it is both raining and not cloudy.

$~~~~~R\implies C ~~\equiv ~~ \neg (R \land \neg C)$

THE TRUTH TABLE

This "definition" is entirely consistent with the usual truth table for logical implication:

From this table we see that:

• If $R$ is true and $R\implies C$ is true (line 1 only), then $C$ is true.
• If $R$ is true and $C$ is false (line 2 only), then $R\implies C$ is false.

These features of the truth table (based on lines 1-2) are often used in both daily discourse and mathematics. The following feature, however, is rarely if ever used in daily discourse:

• If $R$ is false (lines 3-4), then $R \implies C$ is false (regardless of the truth value of $C$)

It is rarely used because little consideration is usually given to the implications the antecedents of which are known to be false. It is, however, often used in very technical arguments (e.g. in mathematical proofs).