0

why do we put the absolute value in the antiderivative of $\int \frac{1}{x}dx = \ln|x|+C $ and not just $\ln(x)+C $

I want to refer that similar questions were asked before here and here

I am a first-year college student who took a course on linear algebra with calculus at the same time. I was puzzled by the fact that we had to use complex numbers in linear algebra, but we were not allowed to use them in calculus. For example, on one side of the test, we had to solve problems involving complex eigenvalues and eigenvectors, but on the other side, we had to ignore the existence of complex numbers and "pretend" that they never existed and use real-valued functions only to me that was very silly but made me wounder about the relationship between complex numbers and calculus especially antiderivatives because this is one of the parts that we ignore the existence of complex numbers by putting the absolute value in antiderivative of $\frac{1}{x}$ . I know that antiderivatives can be generalized to the complex domain using complex analysis, but I have not studied that subject yet (and I may never do so in college). However, I have seen some examples of antiderivatives involving complex numbers on the internet and since antiderivative can be generalised in the complex world isn't that weird to make $\int \frac{1}{x}dx = \ln|x|+C $ and that would make antiderivative with complex numbers meaningless (as the absolute value of any complex number is real number ), also wolfram alpha don't put the absolute value and give the message "assuming a complex-valued logarithm " so that got me thinking if we generalise antiderivative in the complex numbers then the antiderivative of $\frac{1}{x}$ is $\ln(x)+C$ and not $\ln|x|+C$ .

I am curious about this question, but I do not have enough background knowledge to answer them myself. Therefore, I decided to ask here, Thank you for your help .

I see there are many different answers in the comments (personally I liked Joe's answer the most), so I decided to put a bounty on this question.

I think many people will want to know the answer to this question, and I think many students have asked themselves about this question before.

I am sorry if the question seemed too basic and elementary for some of you but as a new math student I struggle with question a lot and I don't have enough experience or knowledge to answer this question.

Xander Henderson
  • 29,772
pie
  • 4,192
  • the integral diverges when it passes through zero, but the idea I believe is to cover the case when both limits of integration are negative (at the same time). think of the area of the graph. – hellofriends Sep 08 '23 at 00:00
  • Simple reason: $\ln x$ is not even defined for $x<0$. – geetha290krm Sep 08 '23 at 00:02
  • @geetha290krm even with considering complex numbers ? – pie Sep 08 '23 at 00:03
  • 5
    @pie: You can define $\ln x$ for when $x$ is a complex number, but it's ... complicated. More to the point, the function you are integrating is implicitly assumed to have a domain of $\mathbb R\setminus{0}$, and so an antiderivative of it should also have that domain (simply because that's part of what "antiderivative" means). Since the complex logarithm is defined for non-real numbers, it is not an antiderivative. – Joe Sep 08 '23 at 00:06
  • @Joe so what does complex integral means if it is not an anti-derivative – pie Sep 08 '23 at 01:10
  • 2
    $\ln|x|+C$ is wrong. Should be $\ln x+C_1$ for $x>0$ and $\ln (-x)+C_2$ for $x<0.$ – Ryszard Szwarc Sep 08 '23 at 07:41
  • 1
    @pie: I think you misunderstood my comment. If you define $\ln$ as a function, say, from $\mathbb C\setminus{0}$ to $\mathbb C$, then its not an antiderivative of the map $f:\mathbb R\setminus{0}\to\mathbb R$ given by $f(x)=1/x$. You can deduce this without calculating anything. Since $f$ has the domain $\mathbb R\setminus{0}$, by definition an antiderivative of $f$ must also have the domain $\mathbb R\setminus{0}$. – Joe Sep 08 '23 at 09:45
  • @RyszardSzwarc I know that , I am asking what is the integral in $\mathbb{C}$ – pie Sep 08 '23 at 12:48
  • If so, the result is $\ln|z|+i{\rm arg} z+c,$ where $c$ is a complex constant and $z\notin (-\infty,0].$ – Ryszard Szwarc Sep 08 '23 at 13:13
  • $\log |x| + C$ is completely wrong for complex variable $x$. Its complex derivative is not $1/x$. But $\log(x)+C$ is correct, where $C$ may be a complex constant. Its complex derivative is $1/x$. – GEdgar Sep 08 '23 at 13:36
  • @GEdgar that what I want to say but now actually I am so confused. there are multiple answers that are different here like the one by
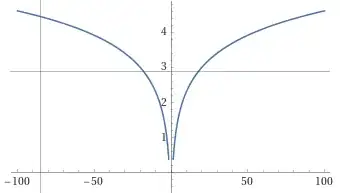
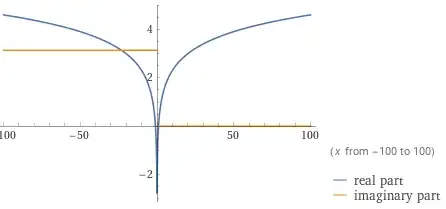
    Ryszard Szwarc or the one by Joe (which honestly I didn't understand) and I don't know what is the the correct answer     – pie Sep 08 '23 at 14:44
  • 1
    @pie: I am happy to clarify anything about my comment that you might confusing. Do you not know what the notation I used means, or is there something else wrong with it? If there are multiple issues, then I am happy to address them all. – Joe Sep 08 '23 at 16:10
  • @GEdgar: It is not possible to define $\log$ as a continuous function on the whole of $\mathbb C\setminus{0}$, though. The map $z\mapsto 1/z$, defined on $\mathbb C\setminus{0}$, does not have an antiderivative. – Joe Sep 08 '23 at 16:16
  • @Joe thank you very much, I didn't understand how does $f(x)= \frac{1}{x}$ doesn't have anti derivative on the from $\mathbb{C}-{0} \to \mathbb{C} $ what I understood is that since f(x) has different domain than the original function then it doesn't count as an anti derivative even though the new function has larger domain. – pie Sep 08 '23 at 17:16
  • 2
    @pie: Showing that there is no map $\mathbb C\setminus{0}\to\mathbb C$ whose derivative is $f(z)=1/z$ is a non-trivial task. You need to use complex analysis for that. But I think this discussion of complex functions is muddying the waters. For one thing, in the context of complex analysis, the definition of the derivative is different in real analysis (even though it similar at first). – Joe Sep 08 '23 at 18:13
  • 2
    You originally asked about a function defined on $\mathbb R\setminus{0}$, and my comment answered why $\ln$ is not an antiderivative–assuming we are talking about real analysis and real derivatives. The indefinite integral of $1/x$ is $\ln|x|+C$ (Ryszard Szwarc's comment has pointed out that even this is a little imprecise, but usually calculus texts gloss over this fact – more discussion is to be found here). – Joe Sep 08 '23 at 18:17
  • 1
    Sorry, in my first comment, in the parenthetical, it should say "even though it looks similar at first". – Joe Sep 08 '23 at 18:22
  • It's not that we can't use complex numbers in calculus, it's that the rules in that case are rather different. Like the real function $f(x)=|x|$ is differentiable everywhere except zero; the complex function $f(x)=|x|$ is not differentiable anywhere. – aschepler Oct 06 '23 at 22:56

3 Answers3

2

The definition of complex logarithm requires much more care than in the real context. This is due to the fact that $$ e^{i\theta} = \cos(\theta) + i \sin(\theta)$$ which, of course, has periodicity $2\pi$. As this is not injective anymore, you cannot define the logarithm as the inverse of this function, because the inverse does not exist!

This is possible only if you choose a determination for its values, and it is comes defined as

$$ \log(r e^{i\theta}) = \log r + i\theta$$

but of course this expressions depends on the determinantion you take for the angle $\theta$. In particular, it comes not defined on some half-line starting from the origin of the complex plane.

Federico T.
  • 963
2

Technically, the “function” $1/x$ over $\mathbb R$ is ambiguous. Rigorously, I mean that to define a proper distribution over $\mathbb R$, you’ll need to be careful in how you treat the singularity. A usual choice is the Cauchy principle value which has the benefit of preserving symmetry. Once the distribution is properly defined, the antiderivative can be calculated unambiguously. Using the Cauchy principal value convention, you can rigorously recover your formula: $$ \int p.v.\frac{dx}{x}= \ln|x|+C $$ Depending on the circumstances, one convention could be more relevant to another. In general, they all differ by an additive Dirac $\delta$ term: $$ \frac{1}{x}=p.v. \frac{1}{x}+A\delta(x) $$ This comes from the fact that $x\delta(x)=0$ and it turns out that it is the only distribution satisfying this property (up to a multiplicative factor). For a chosen $A$, the antiderivative will be: $$ \int \frac{dx}{x}= \ln|x|+AH(x)+C $$ with $H$ the Heaviside function. In short, the antiderivative will generally pick an additional discontinuity at $0$ depending on how you define the inverse.

Other regularizations are more natural from complex analysis. A usual regularization consists in avoiding the pole by the upper/lower half complex plane. This leads to the convention $A=\pm i\pi$ (in physics, you interpret them as causal/anticausal solutions).

When wanting to define the complex antiderivative, holonomy is a fundamental obstacle. The issue is that the antiderivative defined as an integral becomes path dependent, so your antiderivative is multivalued. This is why the complex logarithm is defined up to an additive $i2\pi \mathbb Z$.

Hope this helps.

LPZ
  • 2,788
0

I think that one of the reasons is that, for most cases, $\ln |x|$ "works" better. First of all, you don't have to deal with complex numbers. Second, it "automatically" works for finding areas under the curve.

The problem with $\ln(x)$ is that (a) you have to deal with complex numbers, and (b) you have to deal with the discontinuity at $x=0$.

Technically, at a discontinuity, you can have different values for $C$. Anyway, this all requires a lot more explanation and doesn't gain much value when working with real numbers. Note that the only difference for between the complex $\ln(x)$ and the $\ln(x)$ for real inputs is an additive (complex) constant on the negative side. You can think of $\ln |x|$ as being identical to $\ln(x)$ but automatically adding $-i\pi$ to the constant on the negative side of the graph.

See the graph of $\ln |x|$:

Graph of ln |x|

See the graph of $\ln(x)$:

Graph of ln(x

Personally, I like the idea of just using $\ln(x)$, but just realize that it introduces a lot of issues and questions students may not be prepared to deal with.

johnnyb
  • 3,509