1

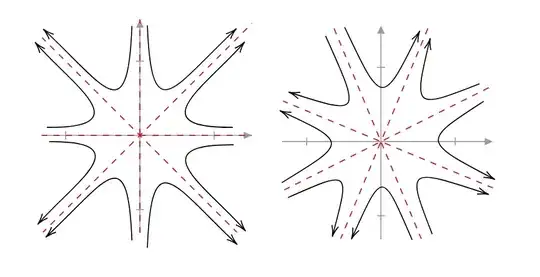
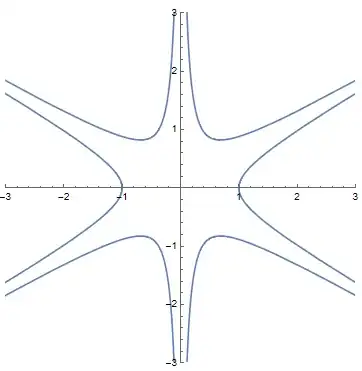
Given that split-complex numbers generates 2D coordinates with 4 asymptotes (when multiplying) that look as follows:

4 asymptotes

The arrows along the hyperbola indicate a positive direction for boosting points along these hyperbola.

Quick explainer: Note that split-complex numbers $\mathbb{D}$ have a $\mathbb{j}$ element such that $\mathbb{j}^2 = 1$. They contrast with the better known complex numbers $\mathbb{C}$ that have an $\mathbb{i}$ element such that $\mathbb{i}^2 = -1$. Thus, you can see that $(x + y\mathbb{j})(a + b\mathbb{j})$ moves a point $(x,y)$ along the hyperbola it lies on if $a + b\mathbb{j}$ is on the special hyperbola passing through the point $1 + 0\mathbb{j}$. In that case $a + b\mathbb{j}$ has a split-complex number magnitude given by $\sqrt{a^2 - b^2} = 1$.

Here's an additional animation to demonstrate boosting along hyperbolas more clearly (python code): animation of boosting

It seems as though there should be an intuitive way to obtain a similar coordinate system with 8 asymptotes instead of 4.

For example, one of: coordinate system with 8 asymptotes

Is there an algebra (or a way to remap split-complex numbers) that would allow one to boost points along these eight hyperbola, or more generally an arbitrary number of hyperbola?

Rehno Lindeque
  • 111

1 Answers1

1

First of all, if you want to construct an algebraic system that extends real numbers, you should have unit "circle" (the set of numbers with magnitude 1) to pass through points (-1,0) and (1,0), because the magnitudes of $1$ and $-1$ are $1$.

Thus, your left bottom picture is not suitable.

As to the right-bottom picture, or other similar, you can construct such algebraic system, but it would not be distributive.

Assume the curve in the bottom right $r(\phi)=\frac{1}{\sqrt{\cos ^2\left(\frac{3 \phi }{2}\right)-\sin ^2\left(\frac{3 \phi }{2}\right)}}$ is the unit circle and define addition as vectors on Euclidean plane, and multiplication in such a way that magnitudes of the vectors multiply and arguments add up. The argument is defined by analogy with complex and split-complex and dual numbers: twice the area of the unit circle (sector) bounded by the given vector's direction.

Now, an arbitrary point, corresponding to a 2-dimensional number on the plane $z=(a,b)$ is characterized by angle $\alpha(z)=\arctan(b/a)$, magnitude $M(z)=\frac{\sqrt{a^2+b^2}}{r(\alpha(z))}$ and argument $\operatorname{arg}(z)=\int_0^{\alpha(z)} r(\phi)^2 d\phi$.

This system will be commutative, associative, but not distributive.

enter image description here

Basically, you can take as a unit circle any curve that is top-bottom and left-right symmetric and crosses points $-1$ and $1$ on the $x$-axis. Then you define multiplication such that magnitudes multiply and arguments add up. You will get a commutative and associative but not distributive algebraic system.

Since multiplication and addition are defined, you can define any analytic functions on this set.

Some of such systems even may have divisors of infinity (non-infinite elements which when multiplied give infinity). For divisors of infinity, you would need the unit circle to cross zero (for instance, having the form of "∞" character).

Additional examples can be found here. You will get interesting systems for lemniscates $r(\phi )=\sqrt{1-a \sin ^2(\phi )}$ with $a$ being $1, 1/2, 2,-1$ (with $a=1$ you get conventional complex numbers).

You can also build a similar system, using taxicab (Manhattan) metric. In Manhattan case, $|(a,b)|=a+b$ and $\operatorname{arg}(a,b)=\frac{2 \arccos \left(\frac{\sqrt{a}}{\sqrt{a+b}}\right)}{\pi (a+b)}$

Anixx
  • 9,119