Thanks to user Blue for pointing out the term "inellipse"—from this pointer I've arrived at a workable formula. To help explain the derivation, here are example diagrams of Triangles $T_0$ and $T$. The value $s_0$ is defined as the half-perimeter of triangle $T_0$.
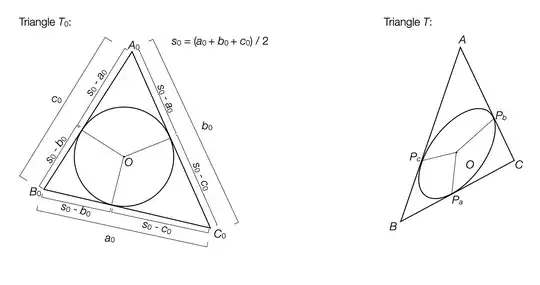
In triangle $T_0$, the lengths of the sides have been labeled and, additionally, the lengths of the segments of the triangle sides formed by splitting each side at the touch-point of the incircle have been labeled. These segment lengths can be derived using Heron's formula and the law of cosines (see the wikipedia page on Heron's formula for a derivation).
Let $\vec{P_a}$, $\vec{P_b}$, and $\vec{P_c}$ be the transformed positions of the three incircle touch-points in triangle $T_0$ (on sides $a_0$, $b_0$, and $c_0$, respectively) to triangle $T$. Because the transformation implied by $\mathbf{M}$ is a linear transformation, the ratio of the two segments on either side of each touch-point must be equal to the ratio of the segments on either side of the transformed touch-points in triangle $T$. So we have:
- $\vec{P_a} = \frac{1}{a_0}\left((s_0 - b_0)\vec{C} + (s_0 - c_0)\vec{B} \right)$
- $\vec{P_b} = \frac{1}{b_0}\left((s_0 - a_0)\vec{C} + (s_0 - c_0)\vec{A} \right)$
- $\vec{P_c} = \frac{1}{c_0}\left((s_0 - a_0)\vec{B} + (s_0 - b_0)\vec{A} \right)$
Using these points, we get the following formulas for conjugate half-diameters, $\vec{f_1}$ and $\vec{f_2}$, of the inellipse.
Let $q = \frac{bc}{\left(s - (a + b)\right)\left(s - (a + c)\right)}$; then:
- $\vec{f_1} = (x_1, y_1) = \frac{\sqrt{q}}{2(q - 1)}\left(\vec{P_b} + \vec{P_c} - 2\vec{P_a}\right)$
- $\vec{f_2} = (x_2, y_2) = \frac{1}{2}\sqrt{\frac{q}{q - 1}}\left(\vec{P_b} - \vec{P_c}\right)$
To obtain the two half-axes $\vec{h_1}$ and $\vec{h_2}$ from these conjugate half-diameters, the answers to this question provide a straightforward method (hat tip to user
Intelligenti pauca). I use an alternative method here that yields the angle $\theta$ as well as the major and minor axis lengths, but that does not require using the singular value decomposition.
Let $\vec{f}(\phi) = \left(x(\phi), y(\phi)\right) = \vec{f_1}\cos(\phi) + \vec{f_2}\sin(\phi)$ be a parametric equation of the ellipse based on the two half-diameters. Then the major and minor half-axes of the ellipse will occur at the minimum and maximum values of $|f(\phi)|^2$. This occurs when its derivative is 0:
$$
\begin{align}
\left|f(\phi)\right|^2 &= \left(x_1\cos(\phi) + x_2\sin(\phi)\right)^2 + \left(y_1\cos(\phi) + y_2\sin(\phi)\right)^2
\\\\
\frac{d}{d\phi}\left|f(\phi)\right|^2 &= \left(2\vec{f_1}\cdot\vec{f_2}\right) \cos(2 \phi) + \left(\left|\vec{f_2}\right|^2 - \left|\vec{f_1}\right|^2\right) \sin(2 \phi) \\\\
\end{align}
$$
By setting the above derivative to 0 and solving, we obtain:
$$ \phi \in \left\{\phi_0 + k\frac{\pi}{2} \Bigm\vert k\in\mathbb{Z}\right\} \\
\phi_0 = \frac{1}{2}\arctan_2\left(2\vec{f_1}\cdot\vec{f_2},\, \left|\vec{f_1}\right|^2 - \left|\vec{f_2}\right|^2\right)$$
(Here, $\arctan_2(\vec{u}) = \arctan_2(y_u, x_u) =$ the angle between the positive x-axis and the vector $\vec{u} = (x_u, y_u)$; note that this is the same as the common atan2(y,x) formulation.)
These values of $\phi$ give us the two half-axes axes of the ellipse:
- $\vec{h_1} = \vec{f}\left(\phi_0\right)$
- $\vec{h_2} = \vec{f}\left(\phi_0 + \frac{\pi}{2}\right)$
From here,
- $\theta = \arctan_2\left(\underset{\vec{h}\in \{\vec{h_1}, \vec{h_2}\}}{\arg\max}\left(\left|\vec{h}\right|\right)\right)$,
- $\alpha = \max\left\{\left|\vec{h_1}\right|,\left|\vec{h_2}\right|\right\}$,
- $\beta = \min\left\{\left|\vec{h_1}\right|, \left|\vec{h_2}\right|\right\}$.
I obtained the formulas for $f_1$ and $f_2$ from Wikipedia's inellipse page, which does not (at time of writing) provide a derivation or reference. I have not derived these formulas myself, but for what it's worth I have tested them empirically.
