0

Problem

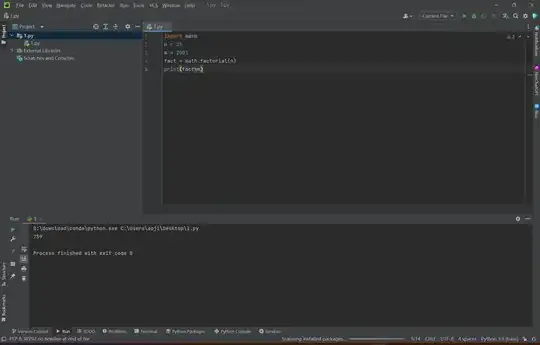
Calculate $x$ so that $x\equiv 25! \mod{2001}$

What I ve tried so far

First of all I came up with the correct solution by splitting the problem up into smaller problems, such as: $$25!\equiv [10!]_{2001} \times [11\times 12 \times 13 \times 14 \times 15]_{2001} \times \cdots \times [23\times 24 \times 25]_{2001} \mod 2001 \equiv [759]_{2001}$$

But this seamed a bit stilted, and I tried: Because of the chinese remainder theorem we find two equations: $$ 25! \equiv b_{69} \mod{69}$$ and $$ 25! \equiv b_{29} \mod{29}$$

Now since $69=3\times 23$ we can split the first equation up again and find that $b_{69}\equiv 0 \mod 69$ For the second equation I did the following: $$25! \equiv b_{29} \mod{29} \iff (-1)(-2)(-3)b_{29} \equiv -6b_{29} \equiv -25!\times 26 \times 27 \times 28 \equiv -28! \mod{29}$$

Now I use Wilsons congruence and find: $$-6b_{29}\equiv (-1)(-1) \mod{29}$$ Now I m just searching for $$b_{29}\equiv [6]_{29}^{-1}$$ and found through Bachet-Bezout $$b_{29}\equiv 5\mod{29}$$

Then I calculated $$ \alpha_{69}\equiv [69]_{29}^{-1}\equiv [8]_{29}$$ And $$\alpha_{29}\equiv[29]_{69}^{-1}\equiv [-19]_{69}$$ And then I thought that $$x\equiv \alpha_{69}b_{29}\times 29 + \alpha_{29}b_{69}\times 69 \equiv 8\times 5\times 29 -19\times 0\times 69 \equiv 1160 \mod{2001}$$

But this is clearly wrong. I would appreciate it very much if someone could help me find my mistake. Thanks

Andreas Caranti
  • 68,873
T_B
  • 155
  • @DietrichBurde Do you mean in a different way as I tried above? If so, could you elaborate on that a bit further please? – T_B Aug 27 '23 at 09:21
  • Thank you! But then I ll get the same solutions as I got above. But how do I add them correctly together? I think I have made a mistake there, because $25! \mod{3} \equiv 25! \mod{23}\equiv 0. And 25! \equiv 5 \mod{29}$ isn’t this correct? Thank you – T_B Aug 27 '23 at 09:28
  • 2
    Sorry, I see you are already using Wilson. The last step is unclear. Of course $25!\equiv 0\bmod 69$, since $3$ and $23$ are divisors of $25!$. And $25!\equiv 5\bmod 29$ is correct. But then? – Dietrich Burde Aug 27 '23 at 09:36
  • And if I have now the solution to both these equations, how do I merge them into an $x\equiv 25! \mod{2001}$ ? – T_B Aug 27 '23 at 09:38
  • 1
    You know already that the remainders of $25!$ modulo $29$, now considered modulo $2001$, are $5,34,63,\ldots, 730,759,\ldots$. So which of these reminders is also divisible by $3$ and $23$? – Dietrich Burde Aug 27 '23 at 09:41
  • Ah, thanks, this really solves my problem: $$ 3\times 23\times k\equiv 5 mod 29$$ and therefore: $$k\equiv 5\times [3]{29^{-1}\times[23]{29}^{-1} \mod{29} $$and with Bachet-Bezout: $$k\equiv 5\times 10 \times (-5) \equiv 11 \mod{29}$$ and therefore $$x\equiv 3\times 23 \times 11 \equiv 759\mod{2001}$$ – T_B Aug 27 '23 at 09:59
  • It's a straightforward application of WR = Wilson Reflection and CRT. ${\rm by\ WR!:}\bmod\color{#c00}{29}!:\ 25!\equiv 1/6\equiv -24/6\equiv -4\equiv \color{#c00}5,,$ so by Easy CRT $$\begin{align}25!&\equiv 0!!!\pmod{!69},\ \ [{\rm by}\ \ 25!\equiv 0 !!!!\pmod{!3\ &\ 23}]\[.2em] &\ \ \ 25!&\equiv\color{#c00}5!!!\pmod{!\color{#c00}{29}}\[.2em] \iff \ 25!&\equiv \underbrace{69\left[\dfrac{5}{11}\bmod 29\right]}_{ 69[\color{darkorange}{11}]\ \equiv\ 759}!!\pmod{!69(29)}\end{align}\qquad\qquad\qquad\ $$ – Bill Dubuque Aug 27 '23 at 17:04
  • we used: $\bmod 29!:\ { \dfrac{1}{11}\overset{\color{#0af}{\rm IR}}\equiv \dfrac{1+3(29)}{11}}\equiv\color{#0a0} 8,,$ so $,{,\dfrac{5}{11}}\equiv 5(\color{#0a0}8)\equiv\color{darkorange}{11},,$ by $,\color{#0af}{\rm IR}=$ Inverse Reciprocity. $\ \ $ – Bill Dubuque Aug 27 '23 at 17:04
  • Btw, another application of Wilson reflection and CRT is the Wilson twin-prime test. – Bill Dubuque Aug 27 '23 at 19:52

2 Answers2

2

\begin{align*} x &\equiv 25! \mod{29} \\ x &\equiv 25!\cdot26\cdot27\cdot28\cdot26^{-1}\cdot27^{-1}\cdot28^{-1} \mod{29} \\ x &\equiv 28! \cdot (26\cdot27\cdot28)^{-1} \mod{29} \\ x &\equiv -1 \cdot 23^{-1} \mod{29} \\ x &\equiv -24 \mod{29} \\ x &\equiv 5 \mod{29}. \end{align*}

Because $3 \mid 25!$ and $23 \mid 25!$, there are ultimately three congruences \begin{align*} x &\equiv 0 \mod{3} \\ x &\equiv 0 \mod{23} \\ x &\equiv 5 \mod{29}. \end{align*}

Their solution is \begin{align*} x &\equiv 0\cdot... + 0\cdot... + 5\cdot3\cdot23\cdot((3\cdot23)^{-1} \mod{29}) \mod{3\cdot23\cdot29} \\ x &\equiv 5\cdot3\cdot23\cdot 8 \mod{2001} \\ x &\equiv 759 \mod{2001}. \\ \end{align*}

Michał
  • 675
  • 1
  • 12
1

I believe you should not calculate $25! \equiv x \mod 29 $, instead, calculate $25! \div69 \equiv x \mod29$ will give you a briefer solution. I will first follow your solution and later point out an easier way of tackling the problem

Indeed, you have correctly calculated that $25! \equiv 5 \mod 29$, and $25! \equiv 0 \mod 69$. Now, you just need to find this $x$ that is divisible by $69$, say $x=69y$ , yet $x \equiv 5 \mod 29$. Which is: $$69 y\equiv5\mod29,$$

using the method of successive division, we can clearly find this $y=11$ in the following process:

$69y\equiv11y\equiv5\mod29$, thus there is a $z$ satisfying $29z\equiv7z\equiv -5 \equiv6 \mod 11$, we can easily find $z=4$, thus $29z+5=121=11y,y=11$.

Hence, $x=11*69=759$.

The second solution just calculates $25! \div69 \equiv x \mod29$, which get $11$ immediately. Let's represent $25!\div 3 \div 23$ as $A$. We can easily get $25! = 69*A$, and since $2001=69*29$, using the associative law of $\textbf{mod}$ operation, $69*A \mod 2001 = 69 *(A\mod29)$.

enter image description here

And python give me the same conclusion.

Leo Ji
  • 144