(Inspired by https://mathoverflow.net/questions/235893/does-there-exist-a-bijection-of-mathbbrn-to-itself-such-that-the-forward-m?rq=1)
Let us define a Darboux function or connected map to be a map between topological spaces that preserves connected sets (i.e. the image of any connected set is connected); and a path-Darboux function or path-connected map to be a map that preserves path-connected sets.
Conjecture: every injective path-connected map $f:[0,1]\hookrightarrow \mathbb R^2$ has to be continuous.
I make several pathetic attempts at this Conjecture below and draw some pictures, but honestly I do not expect nor wish anyone to do anything more than barely skim through them.
Preliminary Remarks:
The converse is of course true: all continuous functions are path-connected maps.
Injectivity is important because of the example of "everywhere locally surjective" functions (functions whose images of any nonempty open set is the entire codomain), like the Conway Base-13 function, or another example using the Riemann rearrangement theorem on the alternating harmonic series.
The Conjecture is true for $f: [0,1] \hookrightarrow \mathbb R$, because we know all discontinuities of Darboux functions are essential, but essential discontinuities contradict injectivity.
If one considers "connected" instead of "path-connected", the Conjecture is false, by considering the graph of the topologist sine curve $g$ with $g(0):=(0,0)$ ($g(t):= (t,\sin(\frac 1t))$ for $t\in (0,1]$).
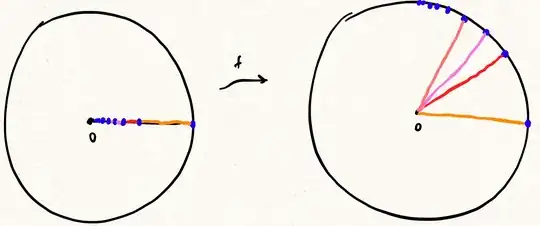
Let us now assume $f$ is not (right-)continuous at $0$, and normalize $f(0)=0$. I think user TheEmptyFunction's answer to the above linked MO post https://mathoverflow.net/a/353018/112504 also applies here to tell us that there are arbitrarily small radii $\epsilon>0$ s.t. there is a sequence $y_n^\epsilon \searrow 0$ s.t. $f(y_n^\epsilon) \in C(0,\epsilon)$ ---- (illustrated below as the blue points, which I think we can normalize via pre-composing with a homeomorphism of $[0,1]$ and post-composing with a homeomorphism of $\mathbb R^2$ to be $\{\frac 1m: m \in \mathbb N^+\}$ in the domain, and $i\cdot e^{-\pi/2 \cdot \frac 1m})$ in the codomain, with $\epsilon=1$)
By mapping $(\frac 1{m+1},\frac 1m]$ to the line segment between $0\in \mathbb C$ (not inclusive) and $i\cdot e^{-\pi/2 \cdot \frac 1m} \in \mathbb C$ (inclusive) in a linear manner say (illustrated above), we get an injective map $[0,1]\to \mathbb R^2$ that maps any interval $[0,a\rangle$ (where the right-hand bracket $\rangle$ denotes both "$)$" and "$]$") to a path-connected set in $\mathbb R^2$ (perhaps we could say this function is a "initial-segment path-connected map"); but any interval $(0,a\rangle$ would not map to a path-connected set.
This example is a "near miss" to the Conjecture.
$$$$
One idea: projection onto 1st and 2nd coordinates are both continuous maps, hence preserve path-connectedness. Thus if $f:=[t\mapsto (x(t),y(t))]:[0,1] \to \mathbb R^2$ is a path-connected map, $x,y:[0,1]\to \mathbb R$ must be as well. As I mentioned above, a well-known class of non-continuous path-connected maps $[0,1]\to \mathbb R$ are the "everywhere locally surjective" functions. By postcomposing with a homeomorphism $\mathbb R \to (0,1)$, we can think of $x,y$ as "everywhere locally surjective" maps $x,y:[0,1]\to (0,1)$.
Then to make $f$ bijective, we need $y$ to be injective when restricted on each fiber $x^{-1}(r)$ for all $r\in \mathbb R$ (where each such fiber is dense in the domain), and vice versa ($x$ injective when restricted to each fiber $y^{-1}(r)$ for all $r\in \mathbb R$). Maybe something like this could work if we can partition $[0,1]$ into disjoint classes $C_\alpha$ where each $C_\alpha \cap x^{-1}(r)$ contains exactly 1 element (so each $C_\alpha$ contains exactly one element that gets mapped to $r$, for each real number $r$), and if $y$ attains a different constant value $c_\alpha$ on each $C_\alpha$. And to make $y$ "everywhere locally surjective" we need each $C_\alpha$ to be dense in $[0,1]$.
However I doubt that such a function preserves path-connectedness; it sends any interval $(a,b)$ (or $[a,b)$, etc.) to a set with lots of pieces of horizontal and vertical lines; if the pieces are too fragmented, we won't get path connectivity. I can imagine that if $y$ was monotone on $x^{-1}(r)$ or something, then we would see a longer vertical line piece at $x=r$; but unfortunately as I commented here this desired monotonicity is not possible.
$$\newcommand{\im}{\operatorname{im}} \newcommand{\harmonicint}[1]{[\frac 1{#1+1},\frac 1{#1}]} \newcommand{\harmonicintt}[1]{[1/({#1+1}),1/{#1}]}$$
Infinitely Many Discontinuities, and Trees
In working with the previous near-miss example, I got the impression that in fact MiniConjecture: one point $p$ of discontinuity of $f$ begets infinitely many points of discontinuity converging to $p$, making such a potential discontinuous $f$ quite difficult to imagine. Unfortunately I could not prove this MiniConjecture.
Attempted proof that 1 discontinuity begets infinitely many:
Since we know that each $[0, \frac 1m]$ maps to a path-connected set containing $f(\frac 1m)$ and $f(0)=0$, let us define:
- paths $P_m : [-\frac 1m, 0] \to f([0, \frac 1m])\subseteq \mathbb R^2$, which we can assume to be injective by e.g. Equivalence of Path-Connectedness and Arc-Connectedness for Hausdorff Spaces, or using Zorn's lemma (article by Jeremy Brazas) --- illustrated below in orange.
- and paths $F_m: [-\frac 1m, - \frac 1{m+1}] \to f([\frac 1{m+1},\frac 1m]) \subseteq \mathbb R^2$ going from $f(\frac 1m)$ to $f(\frac 1{m+1})$ (which we can again assume injective; and furthermore because $f$ is injective, the paths $F_m$ will be disjoint except touching perhaps at endpoints $f(\frac 1m)$) --- illustrated below in green.
Now if $f|_{[1/(m+1),1/m]}$ is continuous as a function $[\frac 1{m+1},\frac 1m]\hookrightarrow \mathbb R^2$, then $f|_{[1/(m+1),1/m]}$ is in fact a homeomorphism onto its image $f(\harmonicint m) \supseteq \im(F_m)$. So its inverse is a continuous map, mapping the path-connected set $\im(F_m)$ to path-connected set in $\harmonicint m$ containing $\frac 1{m+1},\frac 1m$ (since the path $F_m$ goes through those points), meaning $f^{-1}$ maps $\im(F_m) \subseteq f(\harmonicint m)$ to all of $\harmonicint m$, implying that $f|_{\harmonicintt m}$ is in fact a continuous bijection (and hence homeomorphism) $\harmonicint m \to \im(F_m) = f(\harmonicint m)$.
So if $f$ is continuous on $(0,\eta)$ for some $\eta>\frac 1M >0$, then all $\harmonicint m$ inside $(0,\eta)$ will be mapped by $f$ to a path from $f(\frac 1{m+1})$ to $f(\frac 1m)$; in other words, $f$ is composed of all these paths $F_m$ stitched together at the endpoints.
Now if I had the injective continuous path $P_M :[-\frac 1M, 0] \hookrightarrow f([0,\frac 1M])$ that goes through $f(\frac 1M)$ and $f(0)=0$, the fact that $f((0,\frac 1M])$ is the continuous image of $(0,1]$ (so a path/"ray" with a perhaps infinite "tail" that may wiggle a lot, but still pass through all of the points $f(\frac 1m)$ illustrated below), intuitively $P_M$ must end up travelling along this "ray".
Then one would hope to get a contradiction because if $P_M$ travels along this ray, then it would be forced to continue to come across the points $f(\frac 1m)$ (blue points in below pictures), and because the points $f(\frac 1m)$ are so far from $f(0)=0$, this would contradict that $P_M$ is a continuous path $[-\frac 1M, 0] \hookrightarrow f([0,\frac 1M])$.
Sadly after making many attempts in which I kept finding mistakes, I gave up trying to prove this MiniConjecture, though I suspect that it can be proven by making the above intuition/hand-waving rigorous. $$$$
In any case, assuming $f:[0,1] \hookrightarrow \mathbb R^2$ has a discontinuity at $p\in [0,1]$ (e.g. $p=0$ as I normalized above), the paths $F_m$ and $P_m$ that are guaranteed (by path-connectedness of the map $f$) make us have a picture that looks like what follows, with the green $F_m$ paths and orange $P_m$ paths. If indeed we have infinitely many points of discontinuity (illustrated in red) converging to $p$ from the right, then each of those points will lead to another version of this tree structure in the codomain (which I have suggested in the small circles around the red points in the codomain).
All images of intervals $[p, p+\eta\rangle$ (where "$\rangle$" refers to both "$)$" and "$]$") will map to such a tree. Subtracting 2 such intervals leads to general intervals $\langle p+\delta, p+\eta\rangle$ which get mapped to a tree like above, with some portion (portions on the left in the above picture) cut off. But if the tree is super "well-connected" with threads weaving throughout the "canopy", I can imagine that the set remains path-connected.
So perhaps the Conjecture above is false, if one can construct an injective map from $[0,1]$ to this fractal tree-like structure.
$%[![simplified path connected tree thingy][8]][8]$