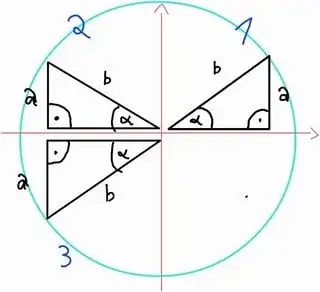
According to Sine - Wolfram Mathworld, Sine is defined as $$\sin(\theta) = \frac{\operatorname{opposite} (a)}{\operatorname{hypotenuse} (b)}$$

From that definition, I don't understand why the sine value in the unit circle in the 3rd quadrant is negative; after all, $a$ and $b$ should both be negative there and a positive quotient follows from this:
People have already explained to me that b is always positive in this case, since it represents the radius and not a vector like a or c (not drawn in here now).
Which leads me to the final question, how is one supposed to actually know that, based on the above definition?
I mean it must be explicitly mentioned somewhere that $b$ in this case represents a length and $a$, $c$ vectors that can take on both positive and negative values; the only thing I see on many pages is that a coordinate system is drawn into the unit circle and hence my obviously wrong assumption.