Construction of a Triangle

Question

The method which I adopt for constructing the triangle is very similar to the method used in the construction of the batman curve.

If you are not familiar with this technique I suggest you look at this answer concerning the construction of the batman curve so you may become familiar with the method.

Okay So I am trying to construct a right-angled triangle. First I start with this equation:

$$|x|+|y|=1$$ This produces a square as such:

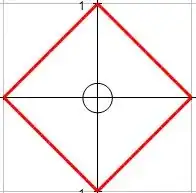
Now to cut this in half I turn the absolute function into it's root representation and swap the square and radical for $x$: $$\left(\sqrt{x}\right)^2+\sqrt{y^2}-1=0$$

that produces this:

Now this is the first part of the equation.

Second part focuses on a line $x=0$ from $x=-1$ to $x=1$. This is what I came up with: $$x\sqrt{1-y^2}=0$$

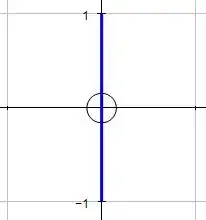
Now in theory I should be able to multiply the two expressions from the LHS of equation $1$ and $2$ to get my desired triangle. However this is not the case and the $2^{\text{nd}}$ expression becomes hidden. However what I have found is that if you add an arbitrarily small value to $x$ it becomes visible but it is not geometrically a triangle. So I have devised a hypothesis about the expression.

$$\left(\left(\sqrt{x}\right)^2+\sqrt{y^2}-1\right)x\sqrt{1-y^2}=0$$ The equation that doesn't work. $$\left(\left(\sqrt{x}\right)^2+\sqrt{y^2}-1\right)\left(\lim_{\epsilon\to0} x + \epsilon\right)\sqrt{1-y^2}=0$$ This is my hypothesis.

So my questions are:

Am I going down the right track in constructing a triangle if so:

• Is there anything I can do to improve my current work?
• Why is it that the second expression gets hidden?

If not:

• What route should I be taking?
• Is there a general equation for a triangle?

Answer 1

The approach is based (correctly) on the fact that setting the product of two expressions $A(x,y),B(x,y)$ to $0$ produces the union of the two curves represented by setting them separately to zero, and also using the fact that $\sqrt{u}$ is only defined for $u \ge 0.$ I can see how your first expression, which I'll call $A(x,y)=(\sqrt{x})^2+\sqrt{y^2}-1$, to zero results in the right half of the square you have drawn in red.

However, in creating the vertical blue segment, you are dealing with imposing two conditions at once: $x=0$ and $-1 \le y \le 1$. Whatever you do for this will involve an intersection (rather than a union) of two zero sets, and maybe the best way to do that if the expressions are $E,F$ is to use the expression $E^2+F^2$, which will capture the intersection of the two relations $E=0,F=0$ when used as a factor. Now to get at the inequality $-1 \le y \le 1$ you could employ the expression $\sqrt{1-y^2}-\sqrt{1-y^2},$ which will be defined exactly when $-1 \le y \le 1$, and will be zero in that interval.

So a version that seems to do the job would be obtained by multiplying the expression giving the right half square by the suggested sum of squares here. This is $$[(\sqrt{x})^2+\sqrt{y^2}-1]\cdot [x^2 + (\sqrt{1-y^2}-\sqrt{1-y^2})^2]=0.$$

ADDED:

The OP Alizter has pointed out in a comment that Wolfram Alpha did not produce the graph correctly using the cooked up second factor here, which involves an expression subtracted from itself internally to the expression. My guess is that the software simplified that part to $0$ before evaluation, and so did not get a reswtriction on $y$. [Note one should be using implicit plot for this equation in $x,y$, maybe with some "tolerance", to have a hope of getting it right.]

So here is another factor designed to capture the vertical line segment: $$B(x,y)=x^2 + (\sqrt{y+1})^2 + (\sqrt{1-y})^2 -2)^2.$$ Then $B(x,y)=0$ iff both of the squared expressions are zero, and the second squared term is undefined when $|y|>1$, and is otherwise zero. So I think the relation $B(x,y)=0$ should produce exactly the vertical line segment joining $(0,-1)$ to $(0,1)$. Using this updated $B(x,y)$, which is hopefully not as likely to be simplified by plotting software, along with the already mentioned factor $A(x,y)$ noted above (and used in OP), the triangle as a whole "should" have equation $A(x,y)\cdot B(x,y)=0.$. I say "should" because I don't know how the software would work on it, and as mentioned I'd suggest at least using some kind of implicit plot, maybe with a tolerance built in to allow for slight errors in a calculated thing being exactly zero.