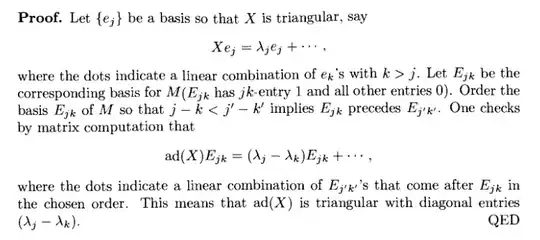0

Prove the following proposition.

If square matrix $X$ has $n$ eigenvalues $\{\lambda_j|j=1,2,\dots,n\}$, then $\operatorname{ad}X (\operatorname{ad}X(Y):=[X,Y]:=XY-YX,\,\forall$ square matrix $Y$ of the same size as $X$) has $n^2$ eigenvalues $\{\lambda_j-\lambda_k|j,k=1,2,\dots,n\}$.

We can prove $\lambda_j-\lambda_k$ is necessarily an eigenvalue of $\operatorname{ad}X$ by picking $Y:=u_j\otimes v_k$ where $u_j$ and $v_k$ are the eigenvectors of $X$ and $X^\dagger$ respectively, such as done in this proof. We need to prove these are all the eigenvalues there are for $\operatorname{ad}X$ as well as their multiplicities.

Here is a proof I do not quite understand. Presumably $M$ in the proof is the operator or its corresponding matrix.

  1. Is $E_{jk}:=u_j\otimes v_k$ where $u_j$ and $v_k$ are the basis vectors of $X$ and $X^\dagger$?
  2. Are we stacking the columns of a matrix into one column matrix (vector) and concatenate all the thus generated large column matrices into a large square matrix? Do we speak of triangle in that matrix? How exactly?

a proof

Hans
  • 9,804
  • To me it looks like in that clipping, $M$ is just the vector space of all $n\times n$-matrices. Nothing with tensor product or stacking or concatenation. It's just a generalization of the proofs in the answers to https://math.stackexchange.com/q/464450/96384. – Torsten Schoeneberg Aug 15 '23 at 00:20
  • @TorstenSchoeneberg: Thank you for the link. I agree with your understanding of $M$. However, both proofs on the linked page are equivalent to my outline above the clip. At least the first proof resorts to tensor product contrary to what you said. Had there been no stacking or something akin to a matrix arrangement, how would you interpret the adjectives "triangular" and "diagonal" in describing $\operatorname{ad}X$? Yes, this problem is "just" a generalization but how? – Hans Aug 15 '23 at 01:42
  • The tensor product is just a way of representing the matrices. In the basis $e_i$, the matrix $E_{i,j}$ (a $1$ in the $i,j$ slot and $0$ elsewhere) is just $e_i \otimes e_j^*$. The terms triangular and diagonal for $\operatorname{ad}X$ are in reference to writing it in the basis $E_{i,j}$ you can call this rearranging if you like (note it is not just stacking the columns, you are told the ordering in that proof). – Callum Aug 15 '23 at 08:43
  • @Callum: I understand what a tensor product is and I even used it to prove the proposition when $X$ is diagonalizable. My question is: when $X$ is not diagonalizable, please describe specifically how $\operatorname{ad}X$ is triangular. – Hans Aug 15 '23 at 12:38
  • 1
    $\operatorname{ad}X$ is an endomorphism on $M$ so can be written as a $\dim M \times \dim M$ matrix by choosing a basis of $M$. It is triangular when you write it in the basis given by $E_{i,j}$ ordered as described in the proof you have included. The proof that is triangular is simply computing $\operatorname{ad}X(E_{i,j})$ and seeing that it only comprises elements in the span of $E_{i,j}$ and other basis elements later in the ordering. This is what it means to be triangular. – Callum Aug 15 '23 at 12:58
  • @Callum: I understand what "triangular" is supposed to mean. But I would like to see the specifics and details. Instead of saying what it supposes to mean, could you please write out the details in terms of the indices of the $\dim M\times \dim M$ matrix and actually show it is indeed triangular as an answer below? – Hans Aug 17 '23 at 03:32

2 Answers2

0

I am a little confused as to which bit you are unsure of in the comments above. I am guessing we just need to connect the dots between the specific form of each $\operatorname{ad}X(E_{i,j})$ and the matrix being triangular.

The fact that $\operatorname{ad}(X)(E_{i,j}) = (\lambda_i - \lambda_j)E_{i,j} + \sum a_{i',j'}E_{i',j'}$ where each $E_{i',j'}$ comes later than $E_{i,j}$ means that the column corresponding to $E_{i,j}$ in the matrix of $\operatorname{ad}X$ has $\lambda_i - \lambda_j$ on the diagonal (the row corresponding to $E_{i,j}$) and $a_{i',j'}$ in the row corresponding to $E_{i',j'}$. Since those come after $E_{i,j}$ in the ordering, those are to the below the diagonal. So the matrix is lower triangular which things of the form $\lambda_i - \lambda_j$ on the diagonal.

If instead it is unclear why $\operatorname{ad}(X)(E_{i,j})$ would have this form you should do some examples. The form of $\operatorname{ad}(X)(E_{i,j})$ is quite specific and when you see it you should be able to prove why it is the case.

Edit: sorry I mixed up my rows and columns above so I have edited it to match the following explanation (the former version made sense if we reversed the order of the basis and would give an upper triangular matrix rather than lower).

So the sticking point seems to be how to translate information written out algebraically into a matrix. Let $A$ be a linear transformation and $x_1,\dots, x_k$ a basis. Writing $A$ a matrix with respect to the $x_i$ is precisely the process of setting $A_{i,j}$ to make $Ax_j=\sum_i A_{i,j}x_i$ true (so $Ax_j$ as a column vector is the $j$th column of the matrix). Now apply that in our scenario. Our basis consists of the $E_{i,j}$ and our transformation is $\operatorname{ad} X$ so if we compute $\operatorname{ad} X(E_{i,j})$ the coefficients of that witten in the basis of the $E_{i,j}$ gives us a column of our matrix. So if the only non-zero coefficients come later than the $E_{i,j}$ one the only non-zero elements in the column come lower than the $E_{i,j}$ one and so on.

Now why do we have this form of $\operatorname{ad} X(E_{i,j})$? I do seriously invite you to actually just compute some examples of the Lie bracket $[X,E_{i,j}]$ as simply the commutator of matrices $XE_{i,j} - E_{i,j}X$ where $X$ is a random lower triangular matrix (doesn't hurt to see what happens on an upper triangular matrix or even any old matrix, either).

You will find that you get a something that looks like:

$$ \left[\begin{pmatrix} *& 0& 0& 0&0 &0\\ *& *& 0& 0& 0&0\\ *& *& * & 0& 0& 0\\ *& *& *& *& 0&0\\ *& *&* & *& *&0\\*& *&* & *&*&*\\ \end{pmatrix}, \begin{pmatrix} 0& 0& 0& 0&0 &0\\ 0& 0& 0& 0& 0&0\\ 0& 0& * & 0& 0& 0\\ 0& 0& 0& 0& 0&0\\ 0& 0&0 & 0& 0&0\\0& 0&0 & 0& 0&0\\ \end{pmatrix}\right] = \begin{pmatrix} 0& 0& 0& 0&0 &0\\ 0& 0& 0& 0& 0&0\\ *& *& * & 0& 0& 0\\ 0& 0& *& 0& 0&0\\ 0& 0&* & 0& 0&0\\0& 0&* & 0& 0&0\\ \end{pmatrix}$$

Specifically, $[X,E_{i,j}]$ is in the span of $E_{i,j}, E_{i+1,j},E_{i+2,j},\dots E_{n,j}, E_{i,j-1}, E_{i,j-2}\dots E_{i,1}$ and $(i+1) - j < i-j$ and so on. You will hopefully notice even more to the pattern such as the entries will be entries pulled right from the matrix $X$ up to sign except for the top right entry which is exactly $X_{j,j} - X_{i,i}$.

So transitioning to our $n^2$ dimensional space $\operatorname{ad} X(E_{i,j}) = (X_{j,j} - X_{i,i})E_{i,j} + a_{i+1,j}E_{i+1,j} + a_{i+2,j}E_{i+2,j} + \cdots$ and so on which as a column vector has $X_{j,j} - X_{i,i}$ as its first non-zero element and that vector is exactly one of the columns of our matrix so that $X_{j,j} - X_{i,i}$ ends up on the diagonal.

Callum
  • 4,321
  • Well, you are just copying the snippet I posted and not adding any details. What is $E_{j,k}$ perhaps in terms of $e_j$? How do you get the expression for $\operatorname{ad}X(E_{j,k})$? You say "Since those come after $E_{i,j}$ in the ordering, those are to the right of the diagonal." Why and how? I do not see it. – Hans Aug 17 '23 at 15:21
  • 1
    @Hans: $E_{j,k}$ is the matrix that has entry $1$ at position $(j,k)$ and $0$ everywhere else. The $E_{j,k}$ form a basis of the space of all matrices, which is the $n^2$-dimensional vector space on which $ad(X)$ acts. (Interpreted as linear map itself (but on the $n$-dimensional vector space with basis $e_1, ... e_n$), $E_{j,k}$ is the map which maps $e_k$ to $e_j$ and every other $e_\ell$ to $0$.) – Torsten Schoeneberg Aug 17 '23 at 16:38
  • @Hans I have added some more explanation – Callum Aug 17 '23 at 17:42
  • Thank you for the matrix diagram. I see $\operatorname{ad}X(E_{i,j})$ being a hokey stick as I have expected, but not triangular. Bear in mind the question is about the triangularity of $\operatorname{ad}X$ (not even the triangularity of $\operatorname{ad}X(E_{i,j})$ which is not triangular anyway). Where is the triangularity except that of $X$ (which is not of concern)? – Hans Aug 18 '23 at 19:55
  • @TorstenSchoeneberg: Yes, I understand that. Please read my comment above to Callum. The question remains: where is the triangularity of $\operatorname{ad}X$? – Hans Aug 18 '23 at 19:59
  • @Hans yes I understand which matrix is supposed to be triangular and I (I feel) clearly explain that above. The matrix diagram shows why $\operatorname{ad}X (E_{i,j})$ has the form shown in the proof. That form tells you that each column of the $\operatorname{ad}X$ matrix has its first non-zero element on the diagonal and that makes the $\operatorname{ad}X$ matrix lower triangular. I'm not really sure what else there is to say. – Callum Aug 18 '23 at 20:57
  • What do you mean by "$\operatorname{ad}X$ matrix"? Where specifically which line in your answer is that matrix? If you have not written it out, can you write it out? How is it "lower triangular"? You can even just give me a numerical example if you can't write it out in abstract. The only matrix I see that is (lower) triangular in your answer is $X$. Which other matrix is triangular? – Hans Aug 18 '23 at 22:22
  • A matrix $[A_{i,j}]{i,j=1}^n$ is lower triangular if and only if $A{i,j}=0, \forall 1\le i<j\le n$. If you say $\operatorname{ad}X$ matrix is indeed lower triangular, please put that matrix in that form. – Hans Aug 18 '23 at 22:27
  • @Hans Can you not see how that definition applies here? The matrix of $\operatorname{ad}X$ is lower triangular because its elements are $A_{(i,j),(i',j')}$ according to some ordering on pairs $(i,j)$ as described, where $A_{(i,j),(i',j')}=0$ whenever $(i,j)<(i',j')$ according to our ordering. – Callum Aug 19 '23 at 01:37
  • @Callum: The explicit demonstration of the impact of the ordering on the triangularity is exactly what I am after, just as stated in my last comment, and wished you would have shown. Unfortunately, your answer does not demonstrate this, explicitly, aside from writing out more details of the matrix multiplication. I have now furnished explicitly the details of the proof in my answer below. – Hans Aug 20 '23 at 07:02
0

Here is the detail of the proof.

In general, a matrix $A$ of a linear transformation $L$ from $M$ to $M$ with basis $\{v_\mu|\mu\in I\}$ for some index set $I$. $Lv_\mu=\sum_{\nu\in I} v_\nu A_{\nu,\mu}$ where $A_{\nu,\mu}$ is the entry of $A$.

Assume $X$ is without loss of generality a lower triangular matrix. This can be achieved via the Schur triangulation or the Jordan canonical form. Now apply the above general formulation to the current problem of $\operatorname{ad}X$. Mapping this problem to the general form described in the second paragraph, we let $L=\operatorname{ad}X, I=\{(i,j), i,j\in\{1,2,\dots,n\}\},\mu:=(j,k)$ and $v_\mu=v_{(j,k)}=E^{j,k},\,v_\nu=v_{(i,m)}=E^{i,m}$. Define order $<$ on $I$ such that $(a,b)<(c,d)$ if $a-b<c-d$. $$A_{\nu,\mu}=A_{(i,m),(j,k)}=\sum_{l=1}^n\big(X_{i,l}E^{j,k}_{l,m}-E^{j,k}_{i,l}X_{l,m}\big) =X_{i,j}\delta_{k,m}-\delta_{i,j}X_{k,m}.$$ $A_{\nu,\mu}=A_{(i,m),(j,k)}\neq0 \implies i>j \wedge k>m\implies i-m>j-k \implies (i,m)>(j,k)$. So $A$ is lower triangular and $A_{\mu,\mu}=A_{(j,k),(j,k)}=X_{j,j}-X_{k,k}$ is an eigenvalue.

Hans
  • 9,804