Modelling with exact differential equations?

Question

I'm teaching some very elementary differential equations to engineering students, and their constant question to me is "What's the use of this?" or alternatively "Where would we use this?" Now, I'm not an applied mathematician, but most of the "standard" applications of de's you see in texts seem to include population growth, radioactive decay, cooling, mixing, predator-prey, all of which can be modelled with separable or linear de's.

So what I'm trying to find is a fairly simple example - suitable to first year students with limited mathematics - of a practical "real-world" application which is most easily modelled by an exact differential equation. My web searching has drawn a blank, so I'm open to suggestions!

Answer 1

I was not sure if you were looking for a linear or a nonlinear. If nonlinear, I would have to think about it more.

You can investigate a series resistor, an inductor, and a capacitor (RLC circuit) in an electrical circuit.

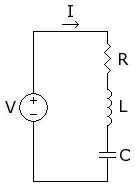
This leads to the differential equation:

$$\displaystyle Ri(t) + L \frac{di}{dt} + \frac{1}{C} \int_{-\infty}^{\tau = t} i(\tau)d\tau = v(t)$$

$$\displaystyle \frac{d^2i(t)}{dt^2} +\frac{R}{L}\frac{di(t)}{dt} + \frac{1}{LC}i(t) = 0$$

You can see this circuit and the analysis on the Wiki. It is a second order system and depending on the type of voltage source, leads to intergro-differential or just differential equation. It is easy to analyze and to understand how it works. This can also be used for projects.

You can see the real life circuit, calculations and the Laplace Transform method to solve on the wiki RLC circuit.

Then you can simulate the results using free tools:

• Computable Data Format from Wolfram to simulate the series RLC circuit and see how the DEQ results match real world parameter settings.
• You can also use this slick Circuit Simulator where you build the circuit using point and click and then simulate it.

Lastly, you could actually breadboard the circuit, get a signal generator, a digital multimeter and oscilloscope and measure it in an actual circuit to see how close the ideal world and real world line up (errors abound in nature).

This gives you a very nice approach because with no cost you can review theory, solve a DEQ, run a simulation in two different environments (or use Modelica) and then actually build and test the circuit for no to little cost.

After doing a series circuit, you can switch to a parallel circuit and then a series-parallel circuit.

These components and circuits are used in every electronic device (including appliances, houses, cars, phones, computers...) that we own.

Answer 2

Any ODE satisfying a conservation law can be written as an exact equation. So I picked the example of a pendulum, which satisfies a non-linear ODE that is very difficult to solve directly: $$\frac{d^2\theta}{d t^2} + \frac{g}{l}\sin\theta =0$$ But the conservation of energy leads to an exact equation $d(\text{Energy})/dt=0$, which can be integrated to give a first-order ODE that is separable: $$ \frac{d\theta}{dt} = \sqrt{{2g\over \ell}\left(\cos\theta-\cos\theta_0\right)} $$

Answer 3

This answer may be helpful but far from real world.

For an application of exact differential equation you may consider problems of orthogonal trajectory. There we used to solve some exact differential equation (But not all problem can be solved only by the method). You may consider their physical interpretation for application. As an example in a two dimensional electrical field the line of force and equipotential curves are orthogonal trajectory of each other.

For non-linear differential equation Prey-Predator model is best to consider. Usually we neglect non-linear terms to model this problem. Consider the interrelation of more than two species your differential equations will be more complicated. Take one or more non-linear terms from taylor series expansion, and get a system of non-linear differential equation. Prey-predator model is one of the highly interesting topic in Bio-math.

One application of differential equation may be interesting to engineering student. Control theory. It is full of differential equation of various kind and their dynamical behaviour.