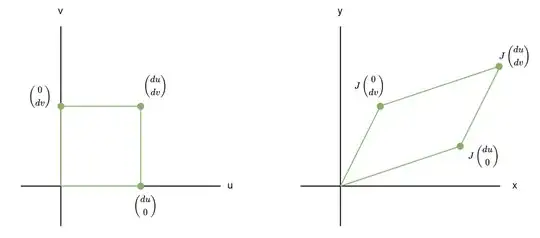
I am currently trying to learn about Jacobians (self study). In particular struggling to understand the geometry of change in variables and why the determinant of the Jacobian is the scaling factor when going from $dudv \to dxdy$.
My current understanding is that the Jacobian represents the best approximation of a linear transformation of the change in a function given a tiny change in its inputs at a given point. At least in my head this makes sense as:
Let: $$ \begin{matrix} x = f_1(u,v) \\ y = f_2(u,v) \end{matrix} $$
Then based on the definition of the Jacobian:
$$ \left(\begin{matrix} dx \\ dy \end{matrix}\right) = J \cdot \left(\begin{matrix} du \\ dv \end{matrix}\right) $$
Where I get lost is how to relate this back to the transformation of $dxdy$. I tried to calculate it as follows though it doesn't work so am assuming I've made (several) invalid steps along the way...
$$ \left(\begin{matrix} dx \\ dy \end{matrix}\right) = J \cdot \left(\begin{matrix} du \\ dv \end{matrix}\right) = \left(\begin{matrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{matrix}\right) \cdot \left(\begin{matrix} du \\ dv \end{matrix}\right) = \left(\begin{matrix} \frac{\partial x}{\partial u} \cdot du\ + \frac{\partial x}{\partial v} \cdot dv \\ \frac{\partial y}{\partial u} \cdot du\ + \frac{\partial y}{\partial v} \cdot dv \end{matrix}\right) $$
Thus:
$$ \begin{align} dxdy &= det\left[ \left(\begin{matrix} dx & 0 \\ 0 & dy \end{matrix}\right) \right]\\ \\&= det\left[ \left(\begin{matrix} \frac{\partial x}{\partial u} \cdot du\ + \frac{\partial x}{\partial v} \cdot dv & 0 \\ 0 & \frac{\partial y}{\partial u} \cdot du\ + \frac{\partial y}{\partial v} \cdot dv \end{matrix}\right) \right] \\ \\&= \left(\frac{\partial x}{\partial u} \cdot du\ + \frac{\partial x}{\partial v} \cdot dv \right) \cdot \left( \frac{\partial y}{\partial u} \cdot du\ + \frac{\partial y}{\partial v} \cdot dv \right) \end{align} \\ \\ \\ = \text{...?} $$
I know that this should resolve to $det(J)dudv$ but I just don't know how to equate that. Any hints / advice on where I might have gone conceptually wrong would be appreciated.
I have already read the answers to similar questions but they haven't helped me clarify where I've gone wrong :(