Why do we stick to single valued functions?

Question

The definition of a function of real variables given in my book was that a function is a rule which assigns to each element in the domain exactly one element of the range. I am new to what a mathematical structure is, but from what I have gathered so far, if I agreed to accept a definition, then I cannot invoke any rules other than those which relate the definition.

Was this structure (definition) imposed to obey the same mathematical structure of algebra (definitions and rules of equality, addition, and multiplication)? For instance, how would we define $\sqrt{4} + 4$ as $+2+4$ or $-2+4$?

From this point of view a multi-valued mapping violates the above definition and cannot be regarded as a function, since a multi-valued mapping assigns to a single element in a set two or more distinct elements of another set.

For example, let $y=\sqrt{x}$. To find its inverse, we break down the curve into a union of single-valued pieces at the points of vertical tangents, which occurs at the origin and consider one branch at a time where the function is bijective. Why do we do this?

Graphically, $\sqrt{4}= \pm 2 $. What is the problem with plotting multiple ordered pairs from the mappings to sketch the curve of $\sqrt{x}$, where $ f:4 \rightarrow \pm 2 $ or $ (4,-2) $ and $ (4,2) $ and forming the inverse by reflecting the graph about y=x.

To clarify in case the readers of this question are confused if it seems I am asking different unrelated questions, what I am trying to say in short is: did we state the existence conditions (injectivity and surjectivity) to take advantage of the mathematical structure and can we use some of the mathematical structure if we violate the definition? Namely graphically, we can plot multivalued functions but can we perform arithmetic without it being ambiguous?

Answer 1

The definition that requires functions to be single valued is so useful in so many contexts that mathematicians don't tinker with it.

So for example, the square root function $\sqrt{\phantom{b}}$ with domain the nonnegative reals always returns the nonnegative root. That doesn't mean the equation $x^2 = 2$ has just one root. It means that if you want to talk about both they are $\sqrt{2}$ and $-\sqrt{2}$.

There are other places in mathematics where you want to study maps from some domain to sets of values in some other domain. You just don't call them “functions”. Or you define them as functions with codomain a set of sets. Or you call them “multi-valued functions”, which is strange from a grammatical point of view but well understood.

(I am pretty sure this is a duplicate question, but can't find the duplicate.)

Answer 2

There was a long-ish blog post relevant to this a few years back by the estimable Tim Gowers, which in turn sparked an extended 64 response discussion.

I'm not going to try to summarise the high spots, as it is nearly all really worth a read.

Here's a link.

Answer 3

This answer is more technical than the level of the question, but hopefully it will be useful to someone. In mathematics, there is a more general concept than a function, namely a relation.

In set theory, a relation from $A$ to $B$ is typically defined as a subset of $A\times B$, and a function $f$ from $A$ to $B$ is defined as a relation from $A$ to $B$ such that (i) for every $a\in A$, there is a $b\in B$ such that $(a,b)\in f$, and (ii) for every $x\in A$ and $y,y'\in B$, if $(x,y)\in f$ and $(x,y')\in f$, then $y=y'$.

Conditions (i) and (ii) imply that if $f$ is a function from $A$ to $B$, then for every $x\in A$, there is one and only one $y\in B$ such that $(x,y)\in f$; this $y$ is written as $f(x)$. However, if all we know is that $f$ is a relation from $A$ to $B$, then for each $x\in A$, it is possible that there is more than one $y\in B$ such that $(x,y)\in f$. It is also possible that there is no $y$ at all such that $(x,y)\in f$! This means that the notation $f(x)$, as defined previously, does not make sense for general relations.

However, there is a way out. Given a relation $f$ from $A$ to $B$ and an $x\in A$, we can define $f(x)$ as follows: $$ f(x)=\{y\in B:(x,y)\in f\} \, . $$ This definition clashes with the previous one if $f$ happens to be a function: if $f(x)=y$ according to the first definition, then $f(x)=\{y\}$ according to the second one. As you can see though, the two definitions are closely linked.

A relation $f$ from $A$ to $B$ thus induces a function $A\to\mathcal P(B),a\mapsto f(a)$ (second definition). In your example, if we make the slightly unorthodox choice of defining the square root as a relation $S$ from $\mathbb R_{\ge0}$ to $\mathbb R$ such that $(x,y)\in S$ if and only if $y^2=x$, then $S$ induces the "multi-valued function" $\varphi:\mathbb R_{\ge0}\to\mathcal P(\mathbb R)$ given by $$ \varphi(x)=\{\sqrt x,-\sqrt x\} \, , $$ where $\sqrt x$ is defined in the usual way. Thus, a real-valued "multi-valued function" can be seen as a bona fide function whose outputs are sets of real numbers.

Although this way of thinking about square roots might seem quite natural, it has some quite serious drawbacks. The first drawback is one you identified in your question, namely that arithmetic with multi-valued functions or relations appears to become ill-defined. Although you could define addition on sets of real numbers, this would feel quite clunky in practice. The second drawback is that concepts such as continuity no longer make sense for multi-valued functions (not unless you define a topology on $\mathcal P(\mathbb R)$, at least, and again there are questions of how useful and natural such a topology would be). The closest one gets to taking the derivative of a multi-valued function in calculus is with the implicit function theorem, and even in this case, the idea is that we can pretend that a multivalued function is single-valued if we "zoom in" enough. Thus, from the standpoint of calculus, relations and multi-valued functions are less fundamental than ordinary functions.

Answer 4

In polar coordinates $(r,\theta)$, the angle $\theta$ is multiple-valued (unless one specifies a interval in which $\theta$ varies). This turns out to be significant in a field such as de Rham cohomology, where understanding that the differential 1-form $d\theta$ on the unit circle is closed but not exact depends on emphasizing the difference between single-valued and multiple-valued.

Answer 5

Anything you can do with multiple-valued "functions", you can do with single-valued functions. This is yet another instance where maths and computer coding really help each other out in terms of understanding the other - it's basically a question of "implementing" the desired functionality using a simpler set of basic tools, like in coding, implementing a binary tree using an array with suitable addressing. And one thing mathematicians like to do is to try and keep the set of basic tools for "implementational" use as simple as possible, hence single-valued functions would be preferred to multi-valued functions as the more basic concept.

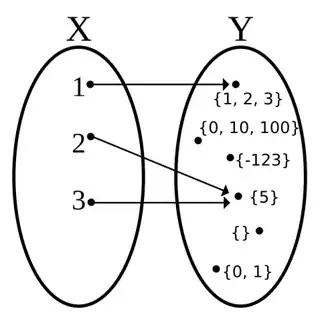
One way to implement multi-valued functions using single-valued ones is to make the codomain of what would be the multi-valued function something other than a number, such that it packages the multiple values together. A common way to do this is to use sets: a "multi-valued function" with domain $D$ and codomain $C$ becomes instead a single-valued function with domain $D$ and codomain $2^C$, so that the multiple output values become bundled together into a single set value. When this definition is in play, the statement $\sqrt{4} = \{ +2, -2 \}$ is true.

Another way to do it, is to keep the codomain as-is, change what the domain of the multi-valued function is. The logic here is that multi-valued functions like $\sqrt{\cdot}$ can be understood as arising from the fact that they are trying to invert "lossy" operations, that is to say, operations (here, squaring) that lose information. Because the information is missing, we cannot unambiguously select a single value with which to define a function. The "codomain" approach, then, basically consists of asking the user of the multi-valued function for more - that is to say, to supply that missing information. A simple way for the square root would be to include along with the number we want to take that square root of, a second variable indicating the sign of the number we presume was squared to create it. Note this is not the same thing as a square root operation taking a signed number as input - rather, it must take a sign and a number separately. There is no standard notation for this - we might be tempted to, say, write $\sqrt{(+, 4)}$, which then is the same thing as "$2$", and $\sqrt{(-, 4)}$, which then is the same as $-2$.

Fortuitously, however, it turns out the notations $\pm \sqrt{n}$ also essentially have an identical effect; and this is likely a reason why we just say "make $\sqrt{n}$ the positive root of $n$ and get it over with". But that isn't the case in more complex cases, e.g. the inverse trigonometric functions, or the complex logarithmic function. In those cases, one may imagine the second argument to be, say, a range in which we are presuming the output angle came from. We might, say, define $\mathrm{arcsin}(a, b; x)$ - again, not a "standard" notation, but one we are introducing to demonstrate the principle - to be the value of the inverse sine of $x$ under the assumption the angle came from the interval $[a, b)$, where we require that $(a, b)$ are subject to the constraints (i.e. limiting the scope of our extended domain), to only those pairs of the form $\left(\left(n - \frac{1}{2}\right) \frac{\tau}{2}, \left(n + \frac{1}{2}\right) \frac{\tau}{2}\right)$, for integers $n$. I.e. $\mathrm{arcsin}(0, 0.3; 1)$, is a domain error.

Of course, there is one more caveat here, and that's that in either case, we often deal with expressions like $2 + \sqrt{4}$ and the like, yet we have a "data type incompatibility" here: if we defined $\sqrt{\cdot}$ in terms of taking a pair with a sign, it is not allowed to take a "$2$" as input, and if we defined it take numbers but produces a set as output, now "$+$" chokes, because it "expected" to take two real numbers, not a real number and a set. Hence, we have to either make some definitions for how we are to, say, promote "$4$" to a pair like $(+, 4)$ - which is, in effect then doing the same thing as simply arbitrarily choosing a single-valued branch, or we have to define how that $+$ is supposed to operate when one of its arguments is not another real number, but a set of real numbers. The latter isn't unheard of at all - typically, the way we do it is just elementwise:

$$a + S := \{ a + s : s \in S \}$$

for adding the real number $a$ and set $S$. Then $2 + \sqrt{4} = \{0, 4\}$ - but the point is, you still have to make this definition and be clear you are doing that, or else, you might run into some form of incorrect mathematical reasoning.

Regardless of the method chosen, however, the point stands: anything you can do with multiple-valued functions you can do with single-valued functions, so that multiple-valued functions provide no greater expressive power to your language. (They also provide no less, since a single-valued function is in effect a degenerate case of a multiple-valued function.) Thus, as a matter of mathematical economy, it's useful to simply not use them, and instead employ single-valued functions more artfully ...

... except that, unfortunately, unlike in computer coding where the compiler ensures our code must conform exactly, maths in practice kind of blurs some of the idealism of the unambiguous formal language it tries to represent into messy notation and usage that is formally nonsense, and thus you will see things where a "multi-valued function symbol" gets tossed around carelessly as though it were a single-valued function. Which can lead to trouble unless you're actually aware of what is going on, which a skilled mathematician will be, but which will cause a learner many hours of frustration with "well what's wrong with it?!" in things like

$$1 = \sqrt{1} = \sqrt{(-1)(-1)} = \sqrt{-1} \sqrt{-1} = i \cdot i = -1.$$

Answer 6

In mathematics, in order to be precise and unambiguous, definitions are often stated in a way that's terse and somewhat abstract; the price we pay for this is that not everything that the definition implies is necessarily immediately obvious - you have to spend some time thinking it through and working things out, building intuition.

The requirement is there to ensure there is no ambiguity on what the result of the function is when you give it a certain input. For the same input, it always returns the same output.

However, stepping outside the realm of real-valued functions of a real variable, and thinking more generally (1, 2), remember that the codomain of a function can be any set. Therefore, the output can be a composite object (in particular, the result itself can be a single object composed of multiple values), or even something that you can use to derive multiple values from it.

For example, the codomain can be a set of ordered pairs. For each input, the function can map to exactly one ordered pair - it's still just one element of the codomain - but then you can extract multiple values from the result.

Here, $f(1) = (-2, 2)$, $f(2) = (1, 1)$ and $f(3) = (1, 1)$. (Image modified from the original here)

Or, something slightly more outlandish, suppose the codomain is a set of triangles expressed as triplets of points in the Cartesian plane - and suppose you have some function mapping each input to a single triangle. Then from the output, you can extract all kinds of results (coordinates, angles, area, ...)

Or, consider something quite common - vector-valued functions: the outputs can be vectors, with any number of dimensions.

The elements of the codomain can also be sets themselves.

You can even have something like a family of related real functions controlled by some parameter as your codomain, and then you can have a function that takes a real number, and for each input outputs a single function from that family. And then you can use the resulting function to extract values by applying it to elements of its domain.

So you can have multiple resulting values "bundled" together, or otherwise somehow encoded. Again, what you can't have is output ambiguity given a certain input.

Similarly, you can have composite objects as inputs. E.g. $f(x, y)$ can be understood as taking a single ordered pair: $f((x, y))$.

Now, when it comes to doing algebra on the reals, if you have a function in there, it's preferable for it to return a real number, to make everything work smoothly. So the output of $\sqrt{\phantom{b}}$ isn't defined to be some composite object like a set or an ordered pair, but rather something that returns a single real value.