0

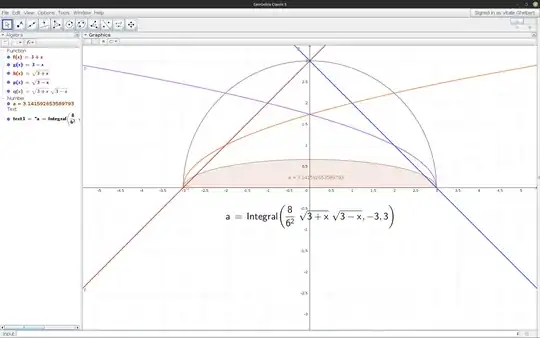
This formula can be simplified?

$$ \pi \sim \frac{8}{n^2} \cdot \sum\limits_{i=0}^{n} \sqrt{i \cdot (n - i)} $$

I am trying to find an alternative formula for circle area.
I stacked to analyze this formula for a while without any progress.

This is not my home work.
I am asking here, because I know all the professional mathematician are here and maybe exist such theorem that I do not know yet and can help to move further with my research.

Thank You.

I tested convergence numerically with:

import math

p = 6
n = 10 ** p


sum_h = 0
for i in range(n+1):
    h = (i * (n - i)) ** (1/2)
    sum_h = sum_h + h


pi0 = 8 * sum_h / n / n


print(" ", math.pi)
print("~", pi0)

  3.141592653589793
~ 3.141592650263593

Here is what I know.

enter image description here

Preview integral example.

enter image description here

We are so close!

enter image description here

  • The sum probably can't be simplified. – jjagmath Aug 03 '23 at 01:18
  • 2
    There is highly unlikely that there is a closed form. However, you can write down an asymptotic expansion $$ S_n \sim \frac{\pi }{8}n^2 +2\zeta \left( -\tfrac{1}{2}\right)n^{1/2}-\zeta \left(-\tfrac{3}{2} \right)n^{ - 1/2} - \frac{1}{4}\zeta \left( { - \tfrac{5}{2}} \right)n^{ - 3/2} - \frac{1}{8}\zeta \left(-\tfrac{7}{2}\right)n^{-5/2}+\ldots $$ for large $n$ in terms of the Riemann zeta function $\zeta$. You can prove this via the polylogarithm generating function ${\rm Li}{-1/2}^2 (z) = \sum{n = 0}^\infty S_n z^n$ and techniques used here. – Gary Aug 03 '23 at 01:47
  • The question has been changed but an asymptotic answer still follows from my comment. – Gary Aug 03 '23 at 01:59
  • @Gary, You correctly answered, that the result is $ \frac{\pi}{8} \cdot n^2 $, but I am looking to simplify this radicals with something simple. –  Aug 03 '23 at 02:05
  • Sometimes there is no simpler solution. – Gary Aug 03 '23 at 02:06
  • 2
    Have you used the fact that you sum is approximately $8\int_0^1\sqrt{x(1-x)}\mathrm{d}x$ when $n$ is large? You can find this integral using elementary methods, and you'll get that it equals $\pi$. – Matthew H. Aug 03 '23 at 02:06
  • @Gary, Yes, but I hope to find something. –  Aug 03 '23 at 02:07
  • @MatthewH., Yes, we can replace almost any sum with integral. You mention a very good point. But if I am not wrong, integral cannot calculate pi value, there are used some series of arcsin or different series of inverse trigonometric functions. True or I must know something new? –  Aug 03 '23 at 02:09
  • @MatthewH. The OP seems to look for a simpler form of the sum and not a simpler way to show the asymptotics. – Gary Aug 03 '23 at 02:09
  • @Vitalie That integral is $B(3/2,3/2)=\pi/8$ in terms of the beta function. – Gary Aug 03 '23 at 02:09
  • @Gary, You are very smart, but I need something simple, as simple that any child can play with. –  Aug 03 '23 at 02:11
  • @Vitalie You have to understand that mathematics is not always simple. You can try to compute the integral by substituting $x=\sin^2 t$, $0<t<\pi/2$. – Gary Aug 03 '23 at 02:12
  • @Gary, Yes, but I need something simple to break this vicious circle. Something that any child will be able to play with and be trivial. I am dreaming to a method that can express circle area as integer value. :) –  Aug 03 '23 at 02:15
  • 2
    @Vitalie The area of the unit circle is $\pi$ which is not an integer. See some formulas here. – Gary Aug 03 '23 at 02:23
  • 5
    The sum $\frac{1}{{n^2 }}\sum\limits_{i = 0}^n {\sqrt {i(n - i)} } = \frac{1}{n}\sum\limits_{i = 0}^n {\sqrt {\frac{i}{n}\left( {1 - \frac{i}{n}} \right)} } $ is a Riemann sum for the integral $\int_0^1\sqrt{x(1-x)}\mathrm{d}x$, whose value is $\pi/8$. This is what you are observing numerically. Read about the Riemann integral. There is no way forward in mathematics if you are not willing to learn and understand new, perhaps more difficult concepts. – Gary Aug 03 '23 at 05:07
  • 1
    Why is this being downvoted? – Captain Chicky Aug 03 '23 at 07:22

3 Answers3

4

@Gary gave in comments the most perfect asymptotic formula you could expect.

Working the asymptotics of a lower bound, consider $$F(n)=\sum\limits_{i=0}^{n} \sqrt{i\,(n - i)}\qquad\text{and}\qquad G(n)=\int_0^{n-1} \sqrt{i\,(n - i)}\,di$$ $$G(n)=\frac{1}{4} \left(n^2 \tan ^{-1}\left(\sqrt{n-1}\right)+(n-2) \sqrt{n-1}\right)$$ For all $n$ the sum is larger than the integral. Recall that $$\int_0^{n} \sqrt{i\,(n - i)}\,di=\frac{\pi }{8}n^2$$

Now, using series expansion, the lower bound is $$G(n)=\frac{\pi }{8}n^2-\frac{2 \sqrt{n}}{3}\left( 1-\frac{3}{10 n}-\frac{3}{56 n^2}-\frac{1}{48 n^3}+O\left(\frac{1}{n^4}\right)\right)$$ which makes $$\frac 8{n^2}F(n)> \pi-\frac{16}{3 n^{3/2}}\left( 1-\frac{3}{10 n}-\frac{3}{56 n^2}-\frac{1}{48 n^3}+O\left(\frac{1}{n^4}\right)\right)$$

For $n=100$, the lhs is $3.13827$ while the rhs is $3.13628$

Claude Leibovici
  • 260,315
0

enter image description here enter image description here

Provided formula $$ \pi \sim \frac{8}{n^2} \cdot \sum\limits_{i=0}^{n} \sqrt{i \cdot (n-i)} $$ is similar with $$ \pi \sim \frac{4}{n^2} \cdot \sum\limits_{i=0}^{n} \sqrt{n^2 - i^2} = \frac{4}{n^2} \cdot \sum\limits_{i=0}^{n} \sqrt{(n+i) \cdot (n-i)} $$

Expressing equivalently with integral

$$ \int_{0}^{n} \sqrt{n-x} \sqrt{n+x} dx = \frac{\pi n^2}{4} $$

0

Using binomial expansion:

$$\int\limits_{0}^{1} \sqrt{1-x^2} dx = \sum\limits_{k=0}^{\infty} (-1)^k \frac{(2k-1)!!}{(2k)!!} \int\limits_{0}^{1} x^{2k}dx$$ $$\int\limits_{0}^{1} \sqrt{1-x^2} dx = \sum\limits_{k=0}^{\infty} (-1)^k \frac{(2k-1)!!}{(2k)!!} \frac{1}{2k+1} \to \frac{\pi}{4}$$