4

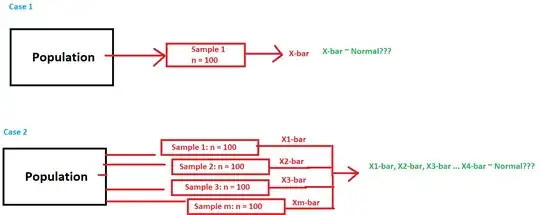
This is a question that I am struggling to understand.

  • Suppose there is a university with 100,000 students (population)
  • I take a sample of 100 students and measure the height of each student
  • Then, I take the average height of these 100 students.
  • Finally, I calculate the variance of this sample average and calculate a 95% Confidence Interval for this sample average

This leads me to my question:

- Even though I interviewed 100 students - effectively, I only have a single sample

  • As I understand, the Central Limit Theorem states that the mean of a (large enough) sequence of samples will be Normally Distributed - Thus, is it correct to use the Central Limit Theorem in this question to construct a Confidence Interval for the average height of the entire population?

In this problem, I understand that I can easily calculate the Standard Deviation of the sample itself - that is, how much does the height of any given student in the sample deviate on average from the average height of all students in the sample.

But in this problem, is it really correct to use the Central Limit Theorem to calculate the Confidence Interval of the average height - when all I have is a single sample?

I think the Central Limit Theorem would be more applicable if many people each took a single sample of size 100 - and then calculated the average height of students in the sample they took. Then, you would have a sequence of sample means - and in this case, the Central Limit Theorem could be used to calculate the Confidence Interval of the sample mean.

Is my reasoning correct?

Thanks!

Note: I have attempted to illustrate both situations - in Case 1, I think the Central Limit Theorem does not apply. In Case 2, I think the Central Limit Theorem does apply:

enter image description here

stats_noob
  • 3,112
  • 4
  • 10
  • 36
  • 1
    for a given large enough sample of size n, $\sqrt n \frac{\overline{x}-\mu}{s_x} $ is a draw from standard normal. This means, we know its behavior as a random variable; and this is the goal of CLT to tell us how the behavior of centered and properly scale random variables (in this case, simple averages) is. – Math-fun Jul 25 '23 at 06:21
  • 1
    You can easily find 100 on-line sources that will tell you that the CLT means that the distribution of the mean of a large sample will approach a normal distribution. But if you look at a statement of the theorem itself, for example https://mathworld.wolfram.com/CentralLimitTheorem.html, you won't find the word "sample" there at all. So I challenge the framing of this question: the CLT does not say anything about the mean of a "large enough sequence of samples", and therefore you are wasting your time looking for an explanation of that misstatement. – David K Jul 27 '23 at 13:29
  • I think you are confused with the meaning of "sample": being true you take a sample of 100 guys, in the "terms" of the CLT each individual guy is a sample of the heights in the population. – Joako Jul 30 '23 at 05:16
  • Why not ? You have taken sample of 100 students which is fairly large to apply CLT which states that the distribution of sample mean of i.i.d random variable is normal. However, the approximations get better and better if you increase the sample size – Dhruv Aggarwal Jul 31 '23 at 14:06

2 Answers2

4

The central limit theorem mainly works for independent identical distributions. In your case you can think of the height of each individual as a random variable. and since we are all humans, it is reasonable to assume that the distributions of our heights are identical. It's also safe to assume that they are independent since the height of student A has nothing to do with student B height. In my opinion, you can think of every individual as an $X_i$, a random variable with a distribution. In general, the most ideal approach would be to weight all 1000 students and calculate the real mean, but in practice it's not always possible to do that with the whole population, because it takes time and in some cases it might be impossible. that's why we choose a random sample of size one hundred. Therefore, theoretically taking 100 students and applying the CLT to the data could be a good approximation, but certainly it's not exact since the CLT is only exact when n approaches infinity. Finally, your approximation gets better and better as you increase n.

Aria
  • 1,445
3

As others have pointed out in the comments, the CLT is perfectly acceptable for a single sample -- the CLT isn't about "samples of samples" or anything like that.

In the classic version, it says that the distribution of the sample mean of $n$ iid random variables, each with mean $\mu$ and standard deviation $\sigma$ approaches that of a normal distribution as the sample sizes get bigger.

More precisely --

$$\sqrt{n}\left[\frac{\left(\frac1n \sum_1^n X_i\right)-\mu}{\sigma}\right] \xrightarrow{d} N(0,1)$$

In terms of probability functions, this is saying:

$$\lim_{n\to \infty} P\left(\sqrt{n}\left[\frac{\left(\frac1n \sum_1^n X_i\right)-\mu}{\sigma}\right] \leq z\right) = \Phi(z)$$

This means that we know larger samples will have "more normal" sample means than smaller ones from the same underlying population.

The big "leap of faith" that we often take in statistics is that we assume that our sample size ($n$) is large enough that

$$\Delta_n:= \max_{z \in \mathbb{R}} \left|P\left(\sqrt{n}\left[\frac{\left(\frac1n \sum_1^n X_i\right)-\mu}{\sigma}\right] \leq z\right) - \Phi(z)\right| \ll 1$$

Most statistical studies are exemplified by Case 1 in your post -- we normally don't artificially split our sample into smaller iid subsamples (unless we are stratifying etc) because we'd get a better estimate using all the data to estimate the mean.

However, if you did do Case 2, you would see that the distribution of the sample means of, say, 1000 (centered and scaled by the mean and standard deviation of the underlying population, respectively) and multiplied by $\sqrt{n}$ would be very close to a standard normal distribution.

You can show this to yourself by running this small snippet of R code:


avgs <- c()
for(i in 1:1000){
  avgs <- append(avgs,mean(runif(1000)))
}

qqnorm(avgs)

You'll see that the sample averages for $n=1000$ is are very normally distributed: enter image description here

Annika
  • 6,873
  • 1
  • 9
  • 20
  • 1
    Thank you so much for your answer! – stats_noob Jul 31 '23 at 04:49
  • @stats_noob Thank You! also, regarding reputable sources -- here is a lecture from Michigan State -- https://stt.msu.edu/Academics/ClassPages/uploads/US19/351-201/Lecture-11.pdf – Annika Jul 31 '23 at 15:02
  • I have always struggled to understand this concept: If I repeat an experiment once and collect a large sample and calculate the mean of this sample ... it is still one sample. Its possible that tomorrow I repeat the same experiment and get a different sample and get a different mean. Thus, I always wondered: in reality, can we confidently apply CLT to a single sample (no matter how large) ? i guess the answer is "yes" ... but I was always unsure about this. – stats_noob Jul 31 '23 at 16:40
  • @stats_noob I agree that its not obvious you can do this -- that is also why the CLT is such an amazing theorem and basically drove the development of classical statistical inference (and it still does!). You are correct that each sample will give you a different sample mean -- what the CLT allows us to assume is that the sample means are normally distributed around the TRUE mean -- in particular $\sqrt{n}\left(\frac{\bar X - \mu}{\sigma}\right)$ has a $N(0,1)$ distribution.

    This is an amazing result because of its specificity and generality.

     – Annika Jul 31 '23 at 16:54
  • @stats_noob -- this relationship is the basis for the confidence intervals for the mean we learn in stats 101.

    Of course, we usually don't know the mean or the standard deviation of our population, so the actual approach also relies on how well we can estimate $\sigma$ using the sample standard deviation.

    If you have a small sample from a normal population, then the $t-$distribution was designed to allow you to form accurate confidence intervals when using $s$ instead of $\sigma$. https://en.wikipedia.org/wiki/Student%27s_t-distribution

     – Annika Jul 31 '23 at 17:01
  • @stats_noob -- bottom line: with moderately sized samples, we are often able to assume (1) that the sample standard deviation is reasonably well estimated and (2) that the sample mean was drawn from a normal distribution with mean $\mu$ and standard deviation $s \approx \sigma$ -- which allows you to form inferences – Annika Jul 31 '23 at 17:05
  • @ Annika: thank you so much for your replies! I am working on a similar question here- can you please take a look at it? https://math.stackexchange.com/questions/4746236/can-the-law-of-large-numbers-be-used-to-prove-convergence-of-moments , https://math.stackexchange.com/questions/4746264/where-does-the-formula-for-the-standard-deviation-come-from thank you so much! – stats_noob Aug 02 '23 at 20:04