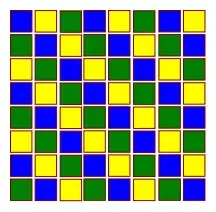
21 tromino tiles (three squares glued together in a row) can together cover 63 squares on an $8 \times 8$ grid. One of the squares thus becomes non-covered. What are the possible positions where the empty square can be?
If this is the relevant object to consider, and it should be arranged only horizontally, being an odd number, it cannot fill any row in the 8x8 grid, without leaving 2 squares unfilled. These two squares are left unfilled for each row, and can be filled by putting a tile on ever row on the empty remaining 2 squares. This leaves one square of the tile outside the 8x8 grid. How can the question assume that 63 squares are filled out of 64, when this combination covers all 64?
Thanks