Here is the sequence formed by concatenating the sequence of prime numbers in base $10$:
$2,3,5,7,\color{red}{1},\color{red}{1},\color{blue}{1},\color{blue}{3},\color{orange}{1},\color{orange}{7},\color{brown}{1},\color{brown}{9},\color{green}{2},\color{green}{3},\dots$
(This is A033308, the sequence of digits in the Copeland-Erdos constant, which is a normal number.)
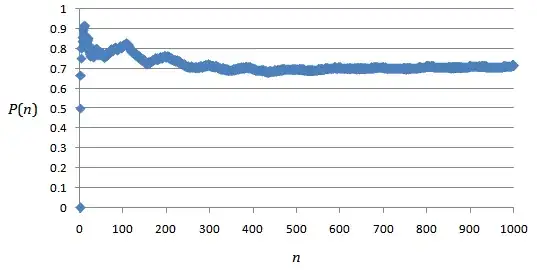
Let $P(n)$ be the proportion of odd terms among the first $n$ terms.
Here is the graph of $P(n)$ against $n$, from $n=1$ to $n=1000$:
Among the first $1000$ terms, the maximum value of $P(n)$ is $P(12)=\frac{11}{12}\approx 0.91667$.
Now consider the following claim:
The absolute maximum value of $P(n)$ is $\frac{11}{12}$.
No one would seriously doubt that the claim is true. Here is some data about the proportion of odd terms in the sequence. For the claim to be false, there would have to be an overwhelming bias toward odd digits deep into the unknown stretches of the prime number sequence, which seems preposterous.
But can the claim be proved?
(If the claim cannot be proved with current knowledge, then this would top my list of intuitively true claims that are unproven; higher on the list than the claim that $\pi+e$ is irrational, and the claim that $\pi$ is normal.)