Do I have a misconception about probability?

Question

I have come across this text recently. I was confused, asked a friend, she was also not certain. Can you explain please? What author is talking about here? I don't understand. Is the problem with the phrase "on average"?

Innumerable misconceptions about probability. For example, suppose I toss a fair coin 100 times. On every “heads”, I take one step to the north. On every “tails”, I take one step to the south. After the 100th step, how far away am I, on average, from where I started? (Most kids – and more than a few teachers – say “zero” ... which is not the right answer.)

In a way it is pointless to talk about misconceptions, when you don't explain the misconceptions...

Source: https://www.av8n.com/physics/pedagogy.htm Section 4.2 Miscellaneous Misconceptions, item number 5

Answer 1

Since the distance can't be negative, the average distance is strictly greater than zero when at least once you don't land on zero.

Let's say you land 2 steps above zero on the first try and 2 steps beneath zero on the second try. Then on average you will have thrown heads and tails equally many times, but the average distance from zero is 2.

How you can see that is as follows: suppose you start with a variable $x$ which is initially 0 and every time you throw heads, you add 1, and every time you throw tails, you subtract 1.

Then the average value of $x$ after 100 throws is 0, since they expect you to throw as many heads as tails on average.

But the average distance is the average value of $|x|$ after 100 throws. Throwing a lot of heads once in one "run" and throwing a lot of tails in another "run" cancels in the average value, but adds to the average distance.

Answer 2

The average distance (in steps) from where you started is approximately $\sqrt{\frac{200}{\pi}}\approx 7.978845608$ and as the number of steps $N$ tends to infinity is asymptotic to $\sqrt{\frac{2N}{\pi}}$.

The "misconception" here is a confusion between the expectation of $S_N=\sum_{i=1}^NX_i$ with $X_i$ independent random variables taking values $\{-1,1\}$ with equal probabilities $\frac{1}{2}$, and the expectation of $|S_N|$; i think this confusion is highly prevalent because we instinctively visualize position and its average, rather than distance, especially because here the symmetry of the random walk draws us to the simple "symmetric" value, $0=-0$. There is another closely related value, simpler to calculate and in some ways more natural: the squareroot of the expectation of $S_N^2$, that is the standard deviation $\sigma$ of $S_N$, as $ES_N=0$.

There are $2^N$ possible paths after N steps, each with probability $2^{-N}$, thus as noted in other answers since all values of the random variable $|S_N|$ are nonnegative, it suffices to find one that is positive to prove that the average distance $E|S_N|>0$. You may take the path $\omega=(1,1,1,...,1,1)$, "all steps to the north": the final distance from where you started is $N$ which contributes $\frac{N}{2^N}$ to the expectation, so $E|S_N|\geq\frac{N}{2^N}>0$.

Hölder's inequality implies that the variance $\sigma^2_{S_N}=ES_N^2\geq (E|S_N|)^2$; and actually $ES_N^2=N$ (by independence of the $X_i$ and $\sigma_{X_i}^2=1$) while as $N\rightarrow\infty$, $(E|S_N|)^2\sim\frac{2N}{\pi}<N$.

The exact formula -whose proof you can find in https://mathworld.wolfram.com/RandomWalk1-Dimensional.html - for $E|S_N|$ is $\frac{(N-1)!!}{(N-2)!!}$, for $N$ even, and $\frac{N!!}{(N-1)!!}$ for $N$ odd. And both formulas have the same asymptotic, given above. As commented by Džuris, the average distance increases only when taking an odd-numbered step -see my reply for a direct proof, not relying on the exact formula, which is not trivial to arrive at.

A decimal approximation of the value (rather than of the asymptotic estimate given at the beginning of this answer) is $E|S_{100}|\approx 7.95892373871787614981270502421704614$, and of course the standard deviation of $S_{100}$ is $10$.

Answer 3

I suspect it comes from the following plausible-sounding but flawed reasoning:

(1) the average final position is the starting point (correct)

(2) so the distance from the starting point to the average final position is zero (correct)

(3) and average distance equals distance to the average (incorrect! the former is actually a much more complicated thing, in this case, than the latter, and they are not equal)

(4) therefore, the average final distance is zero (incorrect)

Answer 4

Is the problem with the phrase "on average"?

Perhaps. You might also be jumping to conclusions about what's being asked. The question says:

After the 100th step, how far away am I, on average, from where I started?

I'm sure you know that to calculate an average, you add all the samples and divide the total by the number of samples. Since the coin is fair, your intuition might tell you that since heads and tails occur with equal frequency, they should cancel each other out and the average distance from the starting point will be zero. However, if you think about all the possible outcomes that you could get from tossing the coin 100 times, the only ones that result in a distance of 0 steps from the start are the ones where there are exactly 50 heads and 50 tails. All the outcomes with more heads than tails or vice versa put you some distance greater than 0 steps from the start, so the average distance has to be more than 0 steps.

Here's a table with all the possible outcomes for just 4 coin tosses, along with their average distance from the start:

As you can see, if you toss a coin 4 times and take 1 step north on heads and 1 step south on tails, on average you'll end up 1.5 steps from the start.

Answer 5

I think the idea here is that most people believe that since you are throwing coin a "large" number of time ($100$ is not large by the way), the heads and tails should "average out" and we should thus be close to the initial point, and that the distance to initial point is $0$.

However, the problem is that this is not how it turns out. What is true is that the ratio between the distance to origin and the total distance walked is trending to $0$ as the number of coin tosses increases. However the average distance to the origin (which can take all values from $0$ to $100$ in our case), is then not $0$.

Answer 6

Flip two coins and walk a mile north for each heads, and a mile south for each tails.
How much is your average cab-fare home?

Phrased this way, we know the answer isn't "zero" because no cabby is going to pay you for walking south instead of north. Doing the math, a quarter of the time you end up 2-miles north, a quarter of the time you end up 2-miles south, and the other half the times you've already made it home; altogether that amounts to 1-mile worth of cab-fare on average. That's not so hard, right?

So what's with the stupid "How far away am I, on average, from where I started?... (Zero is wrong...)" wording? If they didn't want to know 'where' I end up on average, they should have asked 'how far'... umm, I mean... well, that's just annoying now isn't it.

---

And that's why it was worded that way! The lesson isn't supposed to be "And now class, we define a single pedantic definition of what 'How far away?' is supposed to mean!" but rather the lesson is that everyday language can sometimes be vague and/or imprecise.

Or at least, that's the usual place where I see this example: in distance-versus-displacement pedagogy.

Connecting this example to "misunderstanding probability" is somewhat unusual, but it's not entirely incorrect either. In one way it illustrates how, just because you can crunch numbers and output a statistic doesn't necessarily mean that you have actually produced the useful data that you think you wanted.

How so? Well, we've determined the average displacement and average distance for this example: on average you end up back where you started, but on average you spend 1-mile worth of cab-fare. If we didn't just work through the math and know exactly what each of those two statistics signified and how they do/don't relate, we might have looked at those numbers and thought... "Why am I paying a cabby for 1-miles on average when I'm 0-miles from home on average?" or even worse "Why on Earth am I paying somebody to drive me 1-mile away from home!?". Both conclusions are total nonsense and we know why (having done all that the math above) but these kinds of conclusions get made quite easily. Knowing that calculating average cab-fare required the average-distance statistic (rather than assuming that average-displacement was the 'same thing') was vital to understanding the whole situation.

Similarly, problems involving combinatorics, probabilities, and statistics will rely on a chain of logical steps being accounted for properly. What if we hadn't properly accounted for TH and HT separately? We would have thought our average cab ride was (2+0+2)/3=1.33-miles long! Probability problems can be notoriously tricky for new students precisely because it can be hard to properly account for every possibility when you barely know what adding versus multiplying probabilities means and you're just winging it.

Answer 7

We can model taking a step to north or south as discrete random variable $X_n\sim\begin{pmatrix}-1 & 1\\ \frac 12 & \frac 12\end{pmatrix}$. We can then look at random variable $S_n = X_1+X_2+\ldots + X_n$ which will tell us our position after $n$ coin tosses.

If you look at $E(S_n)$, then it is indeed $0$ because $E(X_i) = 0$ and expected value is linear. However, if we want to look at distance from the origin, we should look at random variable $|S_n|$ instead.

Let me assume that $n$ is even, since in the original question we have $n = 100$. The case when $n$ is odd is dealt with similarly. The reason that we consider parity is because $S_n$ is the sum of $n$ odd numbers, so the parity of $S_n$ is the same as $n$. We can look at the probability that $S_n = 2k$, $k = -n/2, -n/2 + 1, \ldots, n/2$. This will happen exactly when there are $n/2+k$ coin tosses that result in heads and $n/2-k$ coin tosses that result in tails. Thus, the probability is $$P(S_n = 2k) = \frac 1{2^n}\binom n{n/2+k}.$$ The expected value of $S_n$ is then $$E(S_n) = \sum_{k=-n/2}^{n/2}\frac 1{2^n}\binom n{n/2+k}\cdot 2k$$ which we can confirm is $0$ by noting that $\binom n{n/2+k} = \binom n{n/2-k}$, so $2k$ and $-2k$ occur equally likely.

The expected value of $|S_n|$, on the other hand is $$E(|S_n|) = \sum_{k=-n/2}^{n/2}\frac 1{2^n}\binom n{n/2+k}\cdot |2k|$$ which is strictly greater than $0$ since $\frac 1{2^n}\binom n{n/2+k}\cdot |2k|>0$ for all $k\neq 0$, and is $0$ for $k = 0$.

Plugging some values of $n$ in software, we get $E(|S_2|) = 1$ (which you can check by hand to convince yourself of the formula), $E(|S_4|) = 1.5$ and $E(|S_{100}|)\approx 7.96.$

I would say the point of the exercise is to understand the difference between $|E(X)|$ and $E(|X|)$, which are not the same in general. In fact $|E(X)|\leq E(|X|)$ is an instance of triangle inequality.

---

The reason that you don't answer to the question "how far am I from home on average" by looking at $S_n$, its expected value and taking absolute value of that is, intuitively, the same reason no one would say the following: "Yesterday I walked two kilometers north from home and today I walked two kilometers south from home. On average, I was at home." One would instead say: "Yesterday I walked two kilometers north from home and today I walked two kilometers south from home. On average, I walked two kilometers from home."

Answer 8

Not right, but perhaps thinking of it this way will help you grasp the problem — you might think of this as where the most people end up, versus the average difference.

Suppose that 98 out of 100 end back where they started, and 1 person was 1 step north, 1 person was 1 step south. That’s still 2% of the total being off, making the average distance be .02 steps. And despite the fair toss, out of a hundred you’re not going to end up with 98 of them back on zero.

Answer 9

The question tries to be kind to the reader by using non-technical language. "How far way am I?", is intended as "what is my positive distance from?", or "how far must I still walk?" or some technical equivalent involving $L_1$ norms. A non-technical reader can easily misinterpret it as "How far North am I?", so the kindness was misplaced. The reader was just confused. There are reasons why professionals use precisely-defined language, and there are many pitfalls involved in communicating with non-professionals

Answer 10

Here is my approach.

Let $X_1,...,X_{100}$ be independent random variables that possess a uniform distribution on $\{-1,1\}$

You're looking to find the expected value of $|X_1+\dots+X_{100}|$.

Put $Y_j=\frac{1}{2}(X_j+1)$. Then $Y_j\sim \text{Bernoulli}(0.5)$ and it follows that $$\mathbb{E}(|X_1+\dots +X_{100}|)=\mathbb{E}\left(|2Y-100|\right)$$

where $$Y=Y_1+\dots+Y_{100}\sim \text{Binom}(100,0.5)$$ Indeed, with the law of the unconscious statistician, the expected value equals $$\sum_{k=0}^{100}|2k-100|{100 \choose k}(0.5)^{100}$$ which is around $7.96$

Answer 11

Okay the question, citation might be incomplete right away.

There are two possibilities in the problem given. One possibility is the mainly discussed one given for the fair coins. The second one, and evidently asked for one is that of the positions taken in the experiment.

Now look detailed into the experiment. The fair coin is thrown and shows a result. Take for example a step to the north. What had been possible before the fair coin is tossed are two results. A step to the north or a step to the south. Each is by the fair coin equally possible. In the second step the conditions change. We get of course the fair possibility for each again in the succession of the two independent tosses. We could stand two steps to the north or south or again where we started. These three results are equally possible so each one has the possibility $\frac{1}{3}$ and we did step a distance different only in one of the results. The case we did not move has the distance zero. In the two other cases we are two steps away. Since the decision is based on the fair coin we use the possibilities for the paths are each equal.

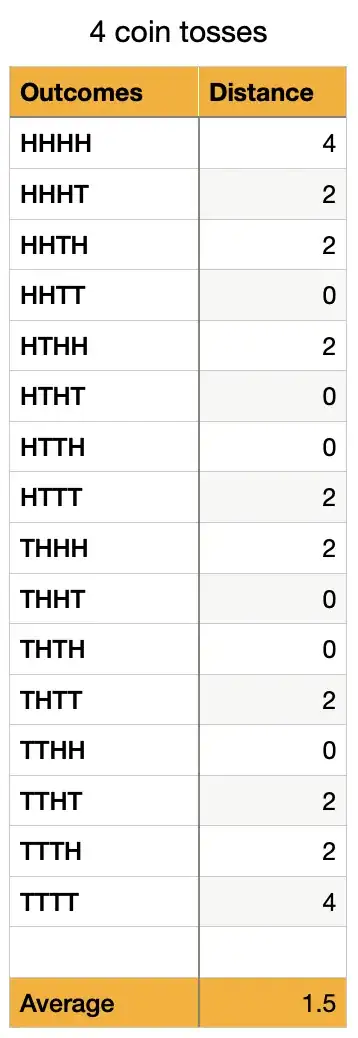
This get more complicated after the third toss. We now get the cases we made three step in one direction, only two times. So our intermediate results has grown again. We now have four results and each one is equally probable. The change is that we do not only ignore negative values in the evaluation of the distance, we get paths that lead to the same position. One step the north, one step to the south and again to the north is still one step to the north altogether.

Mind again the even step place are not taken in the odd steps situation. We change from $\{-2,0,2\}$ to $\{-3,-1,1,3\}$ in the set of taken positions. The distances taken are $\{1,3\}$. These are more possible from the probability at the moment of evaluation than in the step before. We have again $\frac{1}{2}=0.5$ If the paths are considered we have now a bigger weight on each.

Probability changes each time the situation in which the probability is consider does change. So the question is for averages. We see from our results, so where we stand after even and odd numbers of tosses is each symmetric to the place we started is north and south remain different.

This for the human accessible statics heuristics for the posed problem.

A professional answer is:

To calculate the average distance from where you started after taking 100 steps based on the coin toss, we can use the concept of expected value in probability.

Let's analyze the situation step by step:

On every "heads," you take one step to the north. On every "tails," you take one step to the south. Since the coin is fair, the probability of getting "heads" or "tails" is 0.5 (50%) for each toss.

After 100 steps, the net distance you move to the north is the number of heads minus the number of tails. Let's call this difference "D."

The expected value of "D" is the average value we expect to obtain after performing the experiment multiple times. Since the coin tosses are independent and fair, the expected value of "D" is zero. This is because, over a large number of trials, you would expect to have an equal number of heads and tails, leading to a net displacement of zero.

However, we want to find the average distance from where you started, which is the absolute value of "D." The absolute value is used because the distance is always positive, regardless of whether you moved north or south.

As a result, after 100 steps, on average, you would be exactly the same distance away from where you started, which is 0 units.

Remember that this result is based on the assumption of a fair coin and an equal number of steps in both directions (north and south).

To analyze the statistics of this problem, we can consider the random variable "X," which represents the net distance you move after 100 steps. As we discussed earlier, "X" will be the difference between the number of heads and the number of tails.

Let's break down the statistics step-by-step:

1. Probability distribution of a single step:

   • The probability of getting "heads" (moving north) on a single toss is P(Heads) = 0.5.
   • The probability of getting "tails" (moving south) on a single toss is P(Tails) = 0.5.

2. Probability distribution of "X" after 100 steps:

   • The probability distribution of "X" will follow a binomial distribution since we have 100 independent Bernoulli trials (coin tosses) with a probability of success (P(Heads)) equal to 0.5.
   • The probability mass function (PMF) of the binomial distribution is given by: P(X = k) = C(n, k) * (P(Heads))^k * (1 - P(Heads))^(n - k), where C(n, k) is the binomial coefficient, given by C(n, k) = n! / (k! * (n - k)!).

3. Expected value (mean) of "X":

   • The expected value of "X" is the mean distance you would be from where you started after 100 steps.
   • For a binomial distribution with parameters n and p, the expected value is given by n * p, where n is the number of trials (100 steps) and p is the probability of success (P(Heads)).

   Therefore, the expected value of "X" is E(X) = 100 * 0.5 = 50.

4. Variance of "X":

   • The variance of "X" represents the spread or dispersion of the net distance.
   • For a binomial distribution with parameters n and p, the variance is given by n * p * (1 - p).

   Therefore, the variance of "X" is Var(X) = 100 * 0.5 * (1 - 0.5) = 25.

5. Standard deviation of "X":

   • The standard deviation of "X" is the square root of the variance.

   Therefore, the standard deviation of "X" is SD(X) = sqrt(25) = 5.

So, the statistics of the problem are as follows:

• Expected value (mean) of "X": 50
• Variance of "X": 25
• Standard deviation of "X": 5

This means that, on average, you would be 50 units away from where you started after 100 steps, with a spread of 5 units in either direction due to the variability caused by the random coin tosses.

This for sure enhanced the number of professional definitions used. This makes the problem really harder and excuse many of the person allegedly accused in the supporting gossip of the question. I think this is worth this proper scientific answer despite it is lengthy.

Since my perceptions and understandings of the question is different to most of the others given here. I start now my concept for an answer:

There are several possible misconceptions that people might have when considering this problem:

Misinterpreting the expected value: One common misconception is to assume that the expected value of 50 means you will end up exactly 50 units away from the starting point after 100 steps. However, the expected value represents the average value over many trials. In reality, you could end up closer or farther away from the starting point in any single run of 100 steps.

Believing the average distance is always zero: Some people might think that, since there are an equal number of steps in each direction (north and south) due to the fair coin, the average distance should be zero. However, this overlooks the fact that the distance is measured as an absolute value, so the final distance is always positive.

Expecting a linear relationship between steps and distance: Another misconception might involve assuming that the average distance increases linearly with the number of steps taken. For example, doubling the number of steps would double the average distance. In reality, the average distance is determined by the expected value (in this case, 50) and doesn't scale linearly with the number of steps.

Thinking that the standard deviation is the distance you'll end up: The standard deviation of 5 might be misinterpreted as the maximum distance you could end up from the starting point. However, the standard deviation represents the spread of the net distance values (positive and negative) around the expected value (50), but it doesn't determine the farthest distance you might reach in any single run.

Assuming the average distance will converge to zero with more steps: Some might believe that if you increase the number of steps (e.g., to 1,000 or 10,000), the average distance would converge to zero. While it's true that the expected value of "X" will scale linearly with the number of steps, it doesn't mean the average distance will always get closer to zero. Due to the spread caused by the random coin tosses, the average distance will likely oscillate around 0.

Expecting a normal distribution of distances: A common misconception might involve assuming that the distribution of distances after 100 steps will be approximately normal (bell-shaped). However, in this case, the distribution follows a binomial distribution, which can have a different shape, especially for a relatively small number of steps like 100.

To overcome these misconceptions, it's essential to understand the concepts of expected value, probability distributions, and the distinction between average (expected value) and individual outcomes. Probability problems can be counterintuitive, and sometimes our intuition might not align with the actual mathematical results. Analyzing the statistics and the underlying probability distributions can help clarify any misconceptions.