3

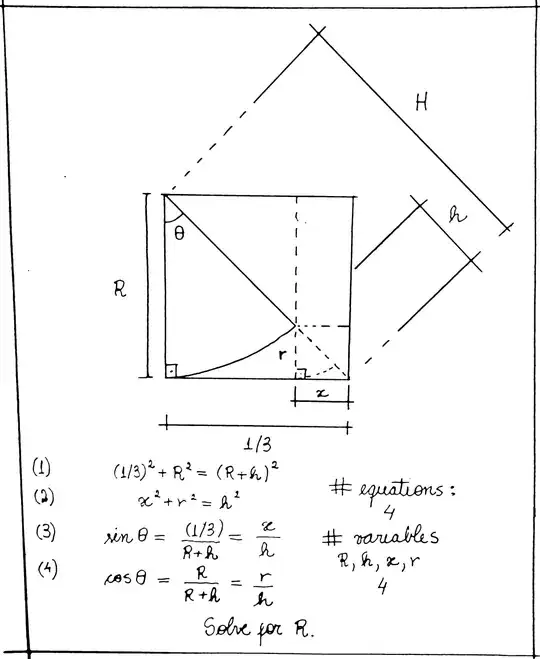
While designing a mechanical part, I stumbled upon a geometry problem that I've been unable to solve. The problem seems simple but the answer has been eluding me.

enter image description here

In the figure, only the base dimension is known (numerically equal to 1/3). There is a circle segment with radius R, marked by the arc, that is formed according to this known dimension. This base dimension is equal to the distance between the tangent point and the intersection of the line when the radius is prolonged.

I need to determine the radius R.

I've assigned variables to the problem as best as possible, and found out four equations to the problem. With four variables and four equations, I thought that the problem was over but got lost in the calculations.

I've also draw this problem in CAD. The program indicated me that it was well defined, and resulted in R = 0.6667. I'm however unable to get to this result analytically.

There is a similar question:

But note that in the case here the arc length is unknown.

Thanks in advance for any assistance.

Paul Frost
  • 76,394
  • 12
  • 43
  • 125
Diego Alves
  • 33
  • 1
    If only the base length of $\frac{1}{3}$ is known then $R$ can be anything. – Paul Jul 23 '23 at 08:28
  • Oh, you are correct. It is clear now. I didn't realize this at first. To make matters worse, made an error using the CAD software that led me to believe that the problem had a unique solution. – Diego Alves Jul 23 '23 at 13:02

2 Answers2

2

The set of equations

$$ \cases{B^2+R^2=(R+h)^2\\ x^2+r^2=h^2\\ \frac{B}{R+h}=\frac xh\\ \frac{R}{R+h}=\frac rh} $$

is dependent. We can obtain the first from the other three. So we should use a reduced set instead as for instance

$$ \cases{B^2+R^2=(R+h)^2\\ x^2+r^2=h^2\\ \frac{R}{R+h}=\frac rh} $$

In this case we obtain

$$ \left\{ \begin{array}{rcl} R&=&\frac{B^2-h^2}{2 h} \\ x&=&\frac{2 B h^2}{B^2+h^2} \\ r&=&\frac{B^2-h^2}{B^2+h^2}h \\ \end{array} \right. $$

Cesareo
  • 33,252
  • Thanks for your answer. You provided the solutions as functions of h and the base dimension, what is also very interesting. and accurate. I wish I could accept your answer too, but JJacquelin elaborated more on how the problem is undetermined. – Diego Alves Jul 23 '23 at 13:12
2

$$(1/3)^2+R^2=(R+h)^2 \tag 1$$ $$x^2+r^2=h^2 \tag 2$$ $$\frac{1/3}{R+h}=\frac{x}{h} \tag 3$$ $$\frac{R}{R+h}=\frac{r}{h} \tag 4$$ From Eq.$(1)$ : $$\boxed{h=-R+\sqrt{R^2+\frac19}}\tag 5$$ From Eq.$(4)$ and Eq.$(5)$ : $$\boxed{r=\frac{R}{\sqrt{R^2+\frac19}}\left(-R+\sqrt{R^2+\frac19} \right)} \tag 6$$ From Eq.$(2)$ and Eqs$(5)$ and $(6)$ : $$\boxed{x=\frac13\frac{-R+\sqrt{R^2+\frac19}}{\sqrt{R^2+\frac19}}}\tag 7$$ One observes that $\frac{Eq.(6)}{Eq.(7)}=\frac{Eq.(4)}{Eq.(3)}=3R=\frac{r}{x}$ which shows that the equations $(1),(2),(3),(4)$ are dependent.

In fact you have not four independent equations but only three. The problem is indetermined.

Giving arbitrary value $R$ one can compute $h,r,x$ which satisfies the four initial equations.

For example with $R=0.666667$ one get $h=0.078689$ , $r=0.070382$ , $x=0.035191$

Or with $R=0.5$ one get $h=0.100925$ , $r=0.083975$ , $x=0.055983$

And so on with other values of $R$.

One more independent equation is necessary in modeling the problem.

JJacquelin
  • 66,221
  • 3
  • 37
  • 87
  • Thanks for the prompt answer. I double checked your calculations and they are correct. You just seem to have missed an equal sign right after you divide the equations, if I'm not mistaken (a typo). it is clear to me now that the problem is undetermined, and you provided answers as functions of R. – Diego Alves Jul 23 '23 at 13:07