Distribution of the largest gap between uniform random variables

Question

I've tried to formulate my question in a previous topic but I terribly messed up my formulation, so I will create a new question to avoid any confusion.

What I'm looking for is the distribution of the maximum gap between two points when I have drawn $n$ samples of iid uniform variates. A "correct" formalized form of the question I have would be the following :

Let $n \geq 2$ be an integer, $a<b$ two real numbers, $X_1, ..., X_n$ be iid $\sim \mathcal{U}([a,b])$ and $X_{(1)}, ..., X_{(n)}$ the corresponding ordered statistics with $X_{(1)} \leq ... \leq X_{(n)}$. For some $\delta \in [0, b-a]$, what would be the value of $$\mathbb{P}\left(\underset{0\leq k \leq n}{\max} \left(X_{(k+1)}-X_{(k)}\right) \leq \delta \right)$$ with the convention $X_{(0)} = a$ and $X_{(n+1)} = b$.

Reducing to the case $a=0$ and $b=1$ :
I know from this wikipedia page that $X_{(k)} \sim Beta(k, n+1-k)$ and that $X_{(k+1)}-X_{(k)} \sim Beta(1, n)$.

This makes the distribution of $X_{(n+1)}-X_{(n)}$ and $X_{(1)}-X_{(0)}$ rather simple to compute with the convention. However it doesn't help me for the maximum as there is no independence.

I found a beginning of answer in the Distribution of maximum gap between points topic. However the answer is incomplete as it mainly is a rewriting of the value as $$\mathbb{P}\left(\underset{0\leq k \leq n}{\max} \left(X_{(k+1)}-X_{(k)}\right) \leq \delta \right) = \mathbb{P}\left(X_{(1)}-X_{(0)} \leq \delta, ..., X_{(n+1)}-X_{(n)} \leq \delta\right)$$

For now I think I will try to brute force with some conditional probabilities, I'll see where it goes. Would anyone have an answer that goes further in the resolution, or another idea on how to deal with this problem ?

EDIT 1 : My brute force method led me to $$\mathbb{P}\left(\underset{0\leq k \leq n}{\max} \left(X_{(k+1)}-X_{(k)}\right) \leq \delta \right) \\ = \\ (1-(1-\delta)^n)^n \cdot \mathbb{P}\left(X_{(1)}\leq \delta | X_{(2)}-X_{(1)}\leq \delta, ..., 1-X_{(n)}\leq \delta \right)$$ However I still don't know how to proceed with that last term.

EDIT 2 : Kimchi lover suggested a very interesting geometric approach before deleting their answer. They pointed that the random vector $\left(X_{(1)}-X_{(0)} , ..., X_{(n+1)}-X_{(n)}\right)$ follows the Dirichelet distribution $D(1, ..., 1)$, therefore giving it a constant density over the $n$-simplex - by noting $\lambda_n$ the $n$-dimensional Lebesgue measure and $\Delta(\delta)$ the set $\{x \in [0,1]^{n+1} : \|x\|_1=1, ~ x_i \leq \delta ~\forall 1\leq i \leq n+1\}$, aforementioned density would be $1/\lambda_n(\Delta(1))$. We now "only" need to compute the size of $\Delta(\delta)$ to then normalize it by $\Delta(1)$.

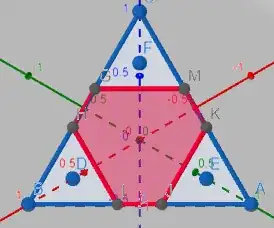
From here I made a drawing - using GeoGebra 3D - of the case $n=2$, $\delta = 0.6$ (left) and $\delta = 0.4$ (right) to get some intuition :

From here I understand there is a critical point at $\delta = 0.5$ as the outer triangles (or $n$-simplex should I say) start to overlap.
To go further I will here stick with the case $\delta \geq 0.5$ :

I understand that I have $n+1$ smaller $n$-simplex with side length $\sqrt{2}(1-\delta)$, therefore giving each of them (cf. https://en.wikipedia.org/wiki/Simplex#Volume) a size of $(\sqrt{2}(1-\delta))^n\frac{\sqrt{n+1}}{\sqrt{2^n}n!}$.
Thus $\Delta(\delta) = \underbrace{(\sqrt{2})^n\frac{\sqrt{n+1}}{\sqrt{2^n}n!}}_{\Delta(1)} - (n+1)(\sqrt{2}(1-\delta))^n\frac{\sqrt{n+1}}{\sqrt{2^n}n!}$.
As such, for $\delta \geq 0.5$ I have : $$\frac{\Delta(\delta)}{\Delta(1)} = 1-(n+1)(1-\delta)^n $$

I will now work on the case $\delta \leq 0.5$, I'd be grateful for any suggestion you might have for it.

EDIT 3 : Following MathSensei's recommendation I looked into formulas for the hyper-area of the intersection between the hypercube $[0,\delta]^{n+1}$ and the hyperplane $\{x\in\mathbb{R}^{n+1} ~:~ \|x\|_1 = 1\}$ when $1/(n+1) \leq \delta \leq 1$.

I found out on the topic Area of the intersection between a hypercube and a hyperplane that the Irwin-Hall distribution has a pdf that corresponds to a very similar version of the problem as it represents the area of the intersection between the hypercube $[0,1]^{n+1}$ and the hyperplane $\{x\in\mathbb{R}^{n+1} ~:~ \|x\|_1 = t\}$. Said pdf is $f(t) = \sum_{i=0}^{n+1} (-1)^i \frac{(n+1)!}{i!(n+1-i)!}\frac{(t-i)^n}{n!}1_{t>i}$.

I naively tried to convert to my problem by multiplying an Irwin-Hall variate $T$ of parameter $n+1$ by $\delta$ to get a new variate $Y = \delta T$ and the equivalent of my hypercube $[0,\delta]^{n+1}$. Its cdf is $F_Y(t) = \mathbb{P}(\delta T \leq t) = \mathbb{P}(T \leq t/\delta) = F_T(t/\delta)$, thus its pdf is $f_Y(x) = f_T(x/\delta)/\delta$.

From here I tried plugging in $x=1$ thinking I would still have that equivalent of intersection with the hyperplane I want and the hypercube, but turns out I'm wrong.

From here I looked for a geometrical proof of the Irwin-Hall pdf that I found for Theorem 1 of section 2 in A geometric derivation of the Irwin-Hall Distribution, Marengo et al. 2017 however I am pretty lost with the $B_j(t)$, especially since I do not want to exclude when coordinates are $>1$ but when they are $>\delta$. I know I would have $t=1$ but they lost me when computing the volume of the intersection of $B_j(t)$.

Answer 1

I'll write here my findings and what I consider to be the answer.

At first I'll stick with the case $[a,b] = [0, 1]$ and generalize at the end.

To begin with, we know from the order statistics wikipedia page that for $1 \leq k \leq n-1, ~ X_{(k+1)} - X_{(k)}$ follows a $Beta(1,n)$, so do $X_{(1)}-0$ and $1-X_{(n)}$ (as $X_{(n)} \sim Beta(n,1)$).

Therefore as @Kimchi lover remarked in a deleted answer, the random vector $X = (X_{(1)} - X_{(0)}, ...,X_{(n+1)} - X_{(n)})$ follows a Dirichlet distribution, with parameter $\alpha = (a_0, ..., a_n) = (1,..., 1)$. Thus its pdf $f(t) = \frac{1}{\text{Beta}(\alpha)} \prod_{k=0}^{n} t_k^{a_k-1}$ is constant and we only need to find an hyper-volume with respect to the Lebesgue measure over $\mathbb{R}^n$ to then rescale it - $\text{Beta}(\alpha)$ is here equal to $1/n!$, it will be important later. The support of this random vector is the $n$-simplex $\{x\in \mathbb{R}^{n+1} ~:~ \|x\|_1=1, x_i \geq 0 ~~ \forall 1 \leq i \leq n+1\}$.

We want to know when all the coordinates are $\leq \delta$, reason why, as @MathSensei suggested, we're looking for the hyper-area of the intersection between the $n$-simplex and the hypercube $[0, \delta]^{n+1}$.

This problem looks very similar to an interpretation of the pdf of the Irwin-Hall distribution for $n+1$ variates I found on the topic Area of the intersection between a hypercube and a hyperplane : $f(t)$ represents the hyper-area of the intersection between the unit hypercube $[0,1]^{n+1}$ and the hyperplane $\{x\in \mathbb{R}^{n+1} ~:~ \|x\|_1=t, x_i \geq 0 ~~ \forall 1 \leq i \leq n+1\}$.
The pdf of such distribution is $f(t) = \sum_{k=0}^{\left\lfloor t \right \rfloor}(-1)^k\binom{n+1}{k}\frac{(t-k)^{n}}{n!}$.

From here I just rescale $T$ a r.v. following an Irwin-Hall distribution by multiplying it by $\delta$ to get individual variables to be uniform over $[0,\delta]^{n+1}$ and find my desired hypercube. I obtain $Y=\delta T$. I now have $F_Y(x) = \mathbb{P}(Y \leq x) = \mathbb{P}(\delta T \leq x) = \mathbb{P}(T \leq x/\delta) = F_T(x/\delta)$. This yields $f_Y(x) = f_T(x/\delta)/\delta$.

From here I get $$f_Y(x) = \frac{1}{\delta}\sum_{k=0}^{\left\lfloor x/\delta \right \rfloor}(-1)^k\binom{n+1}{k}\frac{(x/\delta-k)^n}{n!} = \sum_{k=0}^{ \left\lfloor x/\delta \right \rfloor }(-1)^k\binom{n+1}{k}\frac{(x-\delta k)^n}{n!\delta^{n+1}}$$ that I divide by $1/n!$ as it was the normalizing constant for my Dirichlet distribution. It yields :$$\sum_{k=0}^{ \left\lfloor x/\delta \right \rfloor }(-1)^k\binom{n+1}{k}\frac{(x-\delta k)^n}{\delta^{n+1}} $$

I'm interested in the case $x=1$, still in regards to my $n$-simplex. I then obtain an unsatisfying formula as it doesn't match with the one I found in my EDIT 2 for the case $n=2$ and $\delta \geq 1/2$. To match it I need to multiply by $\delta^{n+1}$, hence my guess at some lack of rigour from me leading to some multiplicative constant missing. That factor must come from a change of variables I probably should have done at some point with a function that simply multiplies each coordinates by $\delta$, thus giving that $\delta^{n+1}$ with the determinant of its Jacobian.

The formula for $X_1,...,X_n$ iid $\sim \mathcal{U}([0,1])$ would be : $$\mathbb{P}\left(\underset{0 \leq k \leq n}{\max} \left( X_{(k+1)}- X_{(k)} \right)\leq \delta \right) = \sum_{k=0}^{\left\lfloor \frac{1}{\delta} \right \rfloor}(-1)^k\binom{n+1}{k}(1-k\delta)^n$$

Do note the support is $[1/(n+1),1]$ as Michael suggested. I have tested it empirically and it seems to be exact. It wasn't rejected when I tested with a KS test (with $n=50$ and a sample size of $1000000$, the $p$-value was $0.23$).

To finish by going back to the general case $[a,b]$, as when $Y \sim \mathcal{U}([a,b])$ we have $X := \frac{Y-a}{b-a} \sim \mathcal{U}([0,1])$. By noting that $Y_{k+1} - Y_k \leq \delta \iff \frac{Y_{k+1}-a}{b-a} - \frac{Y_k -a}{b-a} \leq \frac{\delta}{b-a}$ the final formula would be :

$$\mathbb{P}\left(\underset{0 \leq k \leq n}{\max} \left( Y_{(k+1)}- Y_{(k)} \right)\leq \delta \right) = \left(\sum_{k=0}^{\left\lfloor \frac{b-a}{\delta}\right\rfloor}(-1)^k\binom{n+1}{k}\left(1-\frac{\delta k}{b-a}\right)^n\right)\mathbb{1}_{\left[\frac{b-a}{n+1},~\infty\right)}(\delta) $$

If anyone has a more rigourous approach to that area of intersection calculation I'd be grateful.