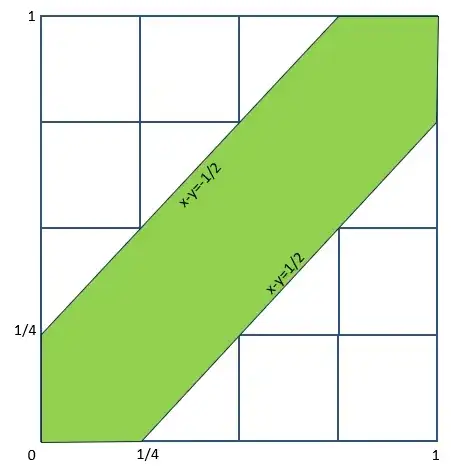
Here is the question I found. We agree to try to meet between 12 and 1 for lunch at our favorite sandwich shop. Because of our busy schedules, neither of us is sure when we’ll arrive; we assume that for each of us our arrival time is uniformly distributed over the hour. So that neither of us has to wait too long, we agree that we will each wait exactly 15 minutes for the other to arrive, and then leave. What is the probability we actually meet each other for lunch? Let random variables X and Y be independent and uniformly distributed the interval [0, 60]. These variables denote the arrival times of the two people during that hour. So, the two people 1 will meet if |X − Y | ≤ 15. Therefore, we compute enter image description here
Can Any one help me to understand how can I get those three different fx(x)?