1

How to construct a smooth modification of the $\log$ function? We want to construct a concrete function $\log^\varepsilon x$ with the following characteristics:

  1. $\log^\varepsilon(x)$ is smooth function in $[0,+\infty)$
  2. $\log^\varepsilon(x)=\log x, \forall x\ge \varepsilon$
  3. $|(\log^\varepsilon(x))'|\le C\cdot 1/x , \forall x\ge 0 $ where $C$ is not depend on $\varepsilon$.
Joako
  • 1,380
Measure32
  • 13

2 Answers2

0

Maybe using a smooth transition function you could built what you want.

As example think of $$q(x)=\dfrac{2}{1+\exp\left({\dfrac{1}{16x^2}}\right)}$$ which is a flat function near zero, this will make the trick.

Now let $f(x)$ be your objective functiom $$f(x)=\log(x)$$

then an smooth approximation will be: $$r(x)=f(x)\cdot q(x)\equiv \dfrac{2\log(x)}{1+\exp\left({\dfrac{1}{16x^2}}\right)}$$

which you could see in Desmos:

example

Joako
  • 1,380
  • 1
    Using Kernel Smoothing may got it, thank you. – Measure32 Jul 21 '23 at 06:03
  • @Measure32 Please consider accepting the answer if it fulfill your expectations. – Joako Jul 22 '23 at 02:02
  • I don't understand how this function satisfies the second criterion. – M. Wind Jul 22 '23 at 05:07
  • @M.Wind it work only as approximation (since the kernel goes to one), but you could do use other smooth transition functions with a steper increase (more elaborated ones). As example, make the smooth bump function $$f(x)=\begin{cases} 1,\ x=0, \ 0,\ |x|\geq 1, \ \dfrac{1}{1+\exp\left(\dfrac{1-2|x|}{x^2-|x|}\right)}\end{cases}$$ then make the smooth transition function $$t(x)=\int\limits_{-\infty}^x f(y)\ dy$$ so you can now make a kernel $$q(x)=t(ax-1)$$ with $a>1$ managing how fast it rises to the value $1$ (so $a$ is related to $\epsilon$), so now $$r(t)=q(x)\log(x)$$ fulfill point 2 – Joako Jul 22 '23 at 06:31
  • @M.Wind you could check it in Desmos, but it takes a lot to load the graphs – Joako Jul 22 '23 at 06:36
  • @M.Wind here in Desmos you could see another slightly simpler example using the classic bump function: $$f(x)=\begin{cases}0,\ |x|\geq 1,\ e^{\frac{x^2}{x^2-1}},\ |x|<1\end{cases}$$ There are plenty of these functions, look them here – Joako Jul 22 '23 at 07:35
  • @Joako $r(t)$ be similarly not in $C^\infty$ – Measure32 Jul 22 '23 at 07:56
  • @Measure32 How not? it will be $C^{\infty}(0,\ +\infty)$ as required: those smooth transition functions goes to zero at $x=0$ in a "much stronger" way that the divergence of any logarythm – Joako Jul 22 '23 at 08:00
  • @Joako I just see the Desmos, I need to check it! – Measure32 Jul 22 '23 at 08:04
  • @Measure32 the relation among $a$ and $\epsilon$ is given just how you manage the scaling and translations of the argument of $q(x)$... I am pretty sure that part could be solved by you since you already know what is a smooth function. – Joako Jul 22 '23 at 08:12
  • @Measure32 even you could avoid using the integral kind of transition function by properly defining piecewise just a half of a bump function with the right-side-half fixed at $1$ forever after, and then translating and scaling it (example here, run faster on Desmos) – Joako Jul 22 '23 at 08:42
  • @Joako Characteristics 3. be similarly hard to satisfied since $(q^\epsilon)'\le C\cdot 1/\epsilon$ – Measure32 Jul 22 '23 at 09:44
  • @Measure32 That is a different requirement that $(q^\epsilon \log(x))'\leq \frac{C}{x},\ \forall x>\epsilon$ – Joako Jul 22 '23 at 15:51
  • @Measure32 even tho last example fulfill $|(q^\epsilon(x) \log(x))'|\leq \frac{1}{x},\ \forall \epsilon>0$ which satisfies condition (3) for $C=1$ – Joako Jul 22 '23 at 15:59
  • @Measure32 I have realized my last statement is wrong, it don't work for every possible positive $\epsilon$, I tried among $\epsilon\in[0.5,\ 10]$ and it works, but for smaller or bigger epsilon indeed could happen its higher than $1/x$. It left to be proved if exist a higher constant $C$ independent from $\epsilon$ that could do the trick. – Joako Jul 23 '23 at 02:40
0

We can achieve this using a cut-off function.

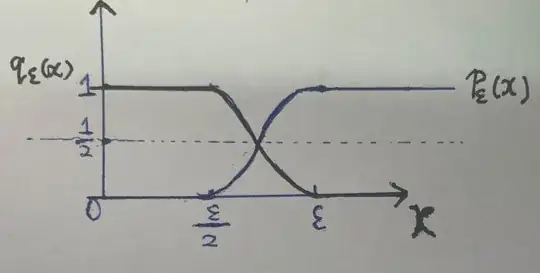
enter image description here

where $p_\epsilon$ is a smooth cut-off function and $(p_\epsilon)'\le \frac{C}{\epsilon}$, $q_\epsilon:=1-p_\epsilon$.

Define $\log^\epsilon(x):=q_\epsilon(x)\log(\epsilon )+p_\epsilon(x)\log(x)$, then $\log^\epsilon(x)$ is a smooth function, $\log(x)=\log^\epsilon(x),\forall x\ge\epsilon$ and \begin{align*} (\log^\epsilon(x))'=&p_\epsilon(x)\frac{1}{x}+\log(\epsilon) q_\epsilon'(x)+p_\epsilon'(x)\log(x)\\ \le& C\frac{1}{x}+(\log(x)-\log(\epsilon))p_\epsilon'(x)\\ \le& C\frac{1}{x}+C|\log(x/\epsilon)|\frac{1}{\epsilon}. \end{align*} We just need to consider the case $\frac{\epsilon}{2}\le x\le \epsilon$, in that case $|\log(x/\epsilon)|\frac{1}{\epsilon}\le C\frac{1}{x}$. So we obtain $$(\log^\epsilon(x))'\le C\frac{1}{x}, \forall x\ge 0,$$ where $C$ is not depend on $\epsilon$.

Xiao Hai
  • 26