why sin of something is always less than that something

Question

I was working on a proof in complex numbers which goes like this:

Let $z_1=r_1\left(\cos \theta_1+i \sin \dot{\theta}_1\right)$ and $z_2=r_2\left(\cos \theta_2+i \sin \theta_2\right)$. Then $\left|z_1\right|=r_1,\left|z_2\right|=r_2, \arg \left(z_1\right)=\theta_1$ and $\arg \left(z_2\right)=\theta_2$. It is given that $\left|z_1\right| \leq 1$ and $\left|z_2\right| \leq 1$. Therefore, $0 \leq r_1 \leq 1$ and $0 \leq r_2 \leq 1$ Now:

\begin{aligned} \left|z_1+z_2\right|^2 & =r_1{ }^2+r_2{ }^2-2 r_1 r_2 \cos \left(\theta_1-\theta_2\right) \\ & =r_1{ }^2+r_2{ }^2-2 r_1 r_2+2 r_1 r_2-2 r_1 r_2\left(\cos \left(\theta_1-\theta_2\right)\right. \\ & =\left(r_1-r_2\right)^2+2 r_1 r_2\left\{1-\cos \left(\theta_1-\theta_2\right)\right\} \\ & =\left(r_1-r_2\right)^2+4 r_1 r_2 \sin ^2\left(\frac{\theta_1-\theta_2}{2}\right) \end{aligned}

$\begin{aligned} & \Rightarrow\left|z_1+z_2\right|^2 \leq\left(r_1-r_2\right)^2+4 \sin ^2\left(\frac{\theta_1-\theta_2}{2}\right)\left[\because r_1=\left|z_1\right| \leq 1\right. \\ & \left.\text { and } r_2=\left|z_2\right| \leq 1\right] \\ & \Rightarrow\left|z_1+z_2\right|^2 \leq\left(r_1-r_2\right)^2+4\left(\frac{\theta_1-\theta_2}{2}\right)^2 \\ & \left.\Rightarrow \mid \because \sin \left(\frac{\theta_1-\theta_2}{2}\right)<\left(\frac{\theta_1-\theta_2}{2}\right)\right] \\ & \Rightarrow\left|z_1+z_2\right|^2 \leq\left(r_1-r_2\right)^2+\left.\left(\theta_1-\theta_2\right)^2\right|^2 \leq\left(\left|z_1\right|-\left|z_2\right|\right)^2+\left\{\arg \left(z_1\right)-\arg \left(z_2\right)\right\}^2\end{aligned}$

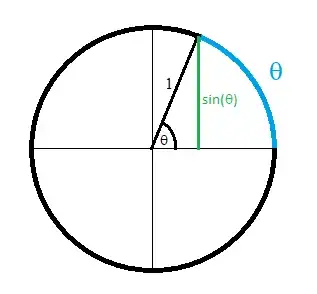
I am not sure why sin of something is always less than that something. as stated in the proof.

So your question is why $\sin x\le x$? Note that this is true only for positive numbers — Andrei, Jul 17 '23 at 15:12
Draw points A and B on the unit circle with center O, extend an altitude down from A meeting OB at C. Then AC<AB<arc(AB). — coiso, Jul 17 '23 at 15:15
See the beginning of this answer to why $(\sin x)/ x \to 1$. — Olius, Jul 17 '23 at 15:15
Where did you get this "proof" from? It is false from the very beginning (take for instance $z_1=z_2=1$). — Anne Bauval, Jul 17 '23 at 15:38

score 1 · Answer 1 · answered Jul 17 '23 at 15:44

1

A visual proof for small $\theta$, as it is obviously true when $\theta>1$ since $\sin(\theta)$ can never be that big

answered Jul 17 '23 at 15:44

Henry

157,058

1

Duplicate of this geometric proof. – Anne Bauval Jul 17 '23 at 15:45

score 0 · Accepted Answer · answered Jul 17 '23 at 15:33

This only requires "proving" when $x \in \left[0, \frac{\pi}2\right]$.

At $x=0$, value of $y=x$ and $y=\sin x$ is equal which is $0$, and slope of $y=x$ is equal to slope of $y=\sin x$ which is $1$.

Now in the specified domain, slope of $y=x$ is constant at $1$, but the slope of $\sin x$ is $\cos x$, which is decreasing from $0$ to $\frac{\pi}2$. So the slope of $\sin x$ keeps dropping. Since $\sin x$ and $x$ started at the same value and slope, this dropping leads to $\sin x<x$ for $x \in \left(0, \frac{\pi}2\right]$, and $\sin x=x$ for $x=0$.

Duplicate of this analytic proof. – Anne Bauval Jul 17 '23 at 15:46 — Anne Bauval, Jul 17 '23 at 15:46

why sin of something is always less than that something

2 Answers2