2

I derived a uniform probability density function (PDF) on a circle, which describes the orientation distribution of fibers on a plane, by dividing the infinitesimal triangular area element of the circle containing fibers oriented in the interval $\left[\varphi, \varphi + d\varphi\right]$, which is the area of a triangle with height $r_{circle}$ (circle radius) and base $dS_{circle} = r_{circle} \cdot d\varphi$ (infinitesimal arc length of a circle), so:

$dA_{circle} = \frac{1}{2} \cdot r_{circle} \cdot dS_{circle} = \frac{1}{2} \cdot r_{circle} \cdot r_{circle} \cdot d\varphi = \frac{1}{2} \cdot r_{circle}^2 \cdot d\varphi$

by the overall area of the circle:

$A_{circle} = \pi \cdot r_{circle}^2$

and equating $dA_{circle}/A_{circle}$ to $P_{uniform,2D}\left(\varphi\right)d\varphi$. This yields the correct PDF:

$P_{uniform,2D}\left(\varphi\right) = \frac{1}{2\pi}$

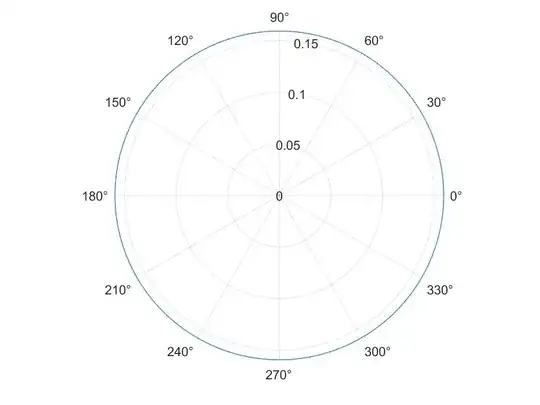
which fulfills the usual normalization condition. A plot of $P_{uniform,2D}\left(\varphi\right) = \frac{1}{2\pi}$ looks circular:

Uniform, two-dimensional PDF

Using the same (geometry-based) derivation path, I get the correct uniform PDF for the sphere:

$P_{uniform,3D}\left(\vartheta,\varphi\right) = \frac{1}{4\pi}$

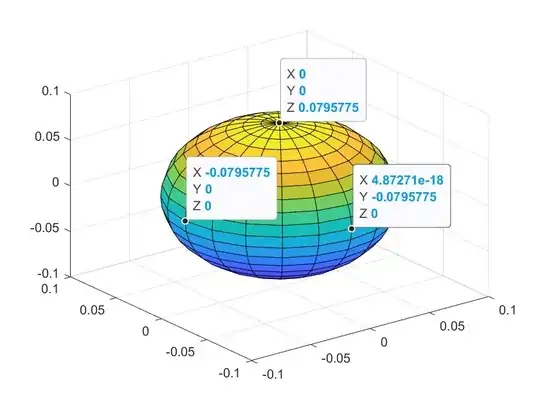
A plot of $P_{uniform,3D}\left(\varphi\right) = \frac{1}{4\pi}$ looks spherical:

Uniform, three-dimensional PDF

Now, I would like to use the same path to derive a nonuniform, two-dimensional PDF defined on an ellipse of given shape.

To do this, I first derived the ellipse radius in polar coordinates by substituting $x$ and $y$ in the "Cartesian expression" for the ellipse:

$\left(\frac{x}{a}\right)^2 + \left(\frac{y}{b}\right)^2 = 1$

by $r\cos(\varphi)$ and $r\sin(\varphi)$, respectively; and solving with respect to $r$. This yields:

$r_{ellipse} = \frac{b}{\left[\sin(\varphi)^2 + \left(b\cos(\varphi)\right)^2\right]^\frac{1}{2}}$

I use "unit ellipses" (as in unit circle, or unit sphere) with $a = 1$, which is why you don't find any occurrences of $a$ in the previous expression.

Then, I also derived the infinitesimal arc length of the ellipse by solving

$ds^2 = \left[\left(\frac{dr}{d\varphi}\right)d\varphi\right]^2 + \left(rd\varphi\right)^2$

and isolating the $d\varphi$ term from the remaiming part of the resulting expression. Specifically, I get:

$dS_{ellipse} = \frac{b^2 \left[ b^4 + \sin(\varphi)^2 - b^4\sin(\varphi)^2 \right]}{\left[b^2 + \sin(\varphi)^2 - b^2\sin(\varphi)^2 \right]^\frac{3}{2}} \cdot d\varphi$

To check the latter, infinitesimal ellipse arc length's correctness I (numerically) integrated $dS_{ellipse}$ over $d\varphi$ from $0$ to $2\pi$ and got results that were identical to those I got via the famous Ramanujan's (analytical) approximations (only for very low values of $0.01$ for the minor semi-axis $b$, did I get relative deviations of $0.34\%$ and for the worst approximation, otherwise virtually identical results, especially for $b \geq 0.3$. All these results also matched that given by the complete elliptical integral of the second kind.

The ellipse area, $A_{ellipse}$, is straightforwardly obtained from:

$A_{ellipse} = \pi b$

Now, the problem is that, if I do:

$\frac{dA_{ellipse}}{A_{ellipse}} = \frac{\left(\frac{1}{2} \cdot r_{ellipse} \cdot dS_{ellipse}\right)}{\pi b} = P_{nonuniform,2D}\left(\varphi\right)d\varphi$

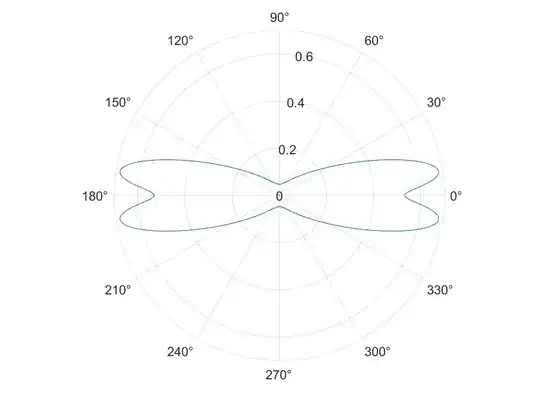
or also with $dS_{ellipse} = r_{ellipse} \cdot d\varphi$ as suggested in the comments below, instead of $dS_{ellipse}$ as in the original expression further above; I either get 1) a PDF that neither exhibits an elliptical shape, nor satisfies the normalization condition (if I use the original $dS_{ellipse}$ expression), here the respective plot:

Nonuniform, two-dimensional PDF 1, b = 0.3

or 2) a PDF that does satisfy the normalization condition, but does not exhibit the shape of an ellipse (if I use the abovementioned $dS_{circle}$ variant), here the respective plot:

Nonuniform, two-dimensional PDF 2, b = 0.3

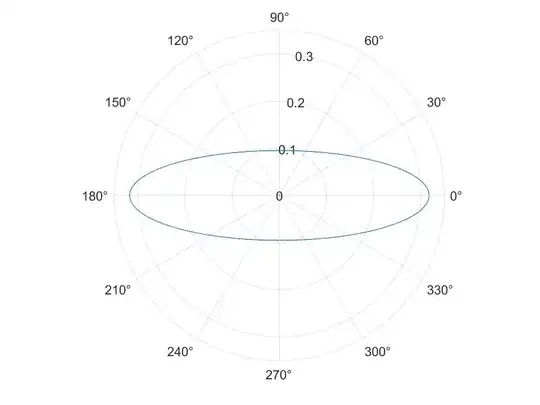
I am insisting with this need for an ellipse-shaped PDF, because I have found (in the literature) a more expedite (also geometry-based) path for deriving the nonuniform, two-dimensional PDF in question, namely by dividing the elliptical radius, $r_{ellipse}$, defined above, by the integral over $\varphi$ of the elliptical radius; so:

$P_{nonuniform,2D}\left(\varphi\right) = \frac{r_{ellipse}}{\int_{0}^{2\pi}r_{ellipse}}$

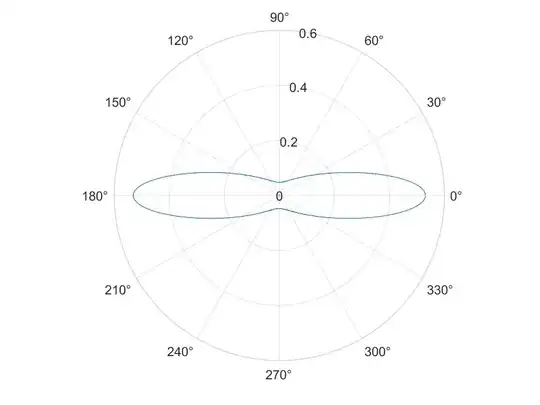
The latter PDF expression exhibits the shape of an ellipse in a polar plot:

Nonuniform, two-dimensional PDF 3, b = 0.3

and satisfies the normalization condition. However, I don't know how theoretically sound this latter derivation path is, which is why I was trying to reach equivalent results via the first, seemingly theoretically sounder derivation path further above.

If this latter, second derivation path is correct and the PDF should indeed exhibit the shape of an ellipse, then I think the only possible explanation for the difficulties with the former, first derivation path is that the expression for the infinitesimal triangular area element containing fibers oriented between $\varphi$ and $d\varphi$ in an ellipse, $dA_{ellipse}$, should be slightly more complicated, mainly because we have more complex infinitesimal triangular area elements (their complexity should in principle more or less match the higher complexity of the the $dS_{ellipse}$ expression vis-a-vis the $dS_{circle}$ expression). I think the infinitesimal triangular area element in question could be given by $dA_{ellipse} = (1/2) \cdot r_{ellipse} \cdot dS_{ellipse} \cdot \sin(\alpha)$, with $\alpha$ the angle between $r_{ellipse}(\varphi)$ and $dS_{ellipse}$, but I'm not completely sure. So, in case this is indeed the correct way of calculating those infinitesimal triangular area elements in the ellipse, my question is: how does one derive an expression for the angle $\alpha$, solely from knowledge of $b$, $r$ and $dS$? Is that possible at all? If it is not: what else could I be doing wrong? If nothing at all, and this geometry-based derivation path is simply not viable for ellipses (or ellipsoids), is there any other (rigorous, perhaps nongeometric) path to derive the sought, elliptical PDF fulfilling the normalization condition?

Another possibility that just occurred to me is that $P\left(\varphi\right)d\varphi$ is only valid for uniform PDFs and perhaps I need to employ some additional normalization factor when deriving nonuniform PDFs. Need to think and probably get deeper into measure and probability theory to rigorously address this issue, if I can't find answers in this forum..............

Euclides
  • 31
  • I have the expression for the infinitesimal arc length, dS. My question is how to compute the area of the infinitesimal triangle with sides r(phi), r(phi + dphi) and dS.............. – Euclides Jul 17 '23 at 14:29
  • Yes, I misread your question. But it is not clear how you derived the ellipse equation in polar coordinates, which you can find here anyway: https://en.wikipedia.org/wiki/Ellipse#Polar_form_relative_to_center – Intelligenti pauca Jul 17 '23 at 14:33
  • I use the elliptical radius to describe/ plot whatever ellipse – Euclides Jul 17 '23 at 14:37
  • I'll add all expressions. Please, give me some time – Euclides Jul 17 '23 at 14:37
  • The area element is the same as before: $dS={1\over2}r(\theta)^2,d\theta$. – Intelligenti pauca Jul 17 '23 at 14:38
  • See https://en.wikipedia.org/wiki/Polar_coordinate_system#Integral_calculus_(area) – Intelligenti pauca Jul 17 '23 at 14:40
  • OK. So, you say I should use the circle area element and divide it by the ellipse area to get my nonuniform PDF, is that correct? But what about $r$ in the $dA$ expression? Elliptical $r$ or circular $r$? – Euclides Jul 17 '23 at 15:06
  • $r(\theta)$ is given by the formula I linked above of the ellipse equation in polar coordinates. – Intelligenti pauca Jul 17 '23 at 15:14
  • yes. I had tried that area element before in combination with the elliptical radius. That was my first attempt actually. I did get a PDF that satisfied the normalization condition. However, that PDF does not exhibit an elliptical shape (rather Cassini oval, wrapped Cauchy, von Mises like; that sort of shape), which is why I decided to test an area element based on the elliptical arc length, which in turn led to the fundamental question of infinitesimal triangular area elements in ellipses....... – Euclides Jul 17 '23 at 15:30
  • What do you mean by "does not exhibit an elliptical shape"? – Intelligenti pauca Jul 17 '23 at 18:11
  • See if this can help you: https://stackoverflow.com/a/46840451 – Intelligenti pauca Jul 17 '23 at 18:15
  • I meant that a plot of $P_{nonuniform, 2D}\left(\varphi\right)d\varphi$ doesn't resemble an ellipse. I'll add plots to my question in the coming hours to facilitate interpretation. I will also take a closer look at the link you suggested. Looks like I could find valuable information therein. Thank you! – Euclides Jul 17 '23 at 19:32
  • If you look at that link, you'll find that using $dA={1\over2}r^2,d\theta$ they find $$p(\theta)={ab\over2\pi((b\cos\theta)^2+(a\sin\theta)^2)}$$ and from there they build a random generator of points, uniformly distributed inside the ellipse. The result looks fine, so I think there is little doubt that is the right PDF. Instead, I don't understand why the PDF should have the shape of an ellipse, as you claim. – Intelligenti pauca Jul 18 '23 at 06:34
  • yes, I saw that. not sure if or why that uniform distribution of random points inside the ellipse is sufficient proof of the PDF's correctness or even uniqueness. I mean, to me, the derivation path leading to the last nonuniform PDF I presented looks conceptually perfectly fine and essentially equivalent to dividing infinitesimal area elements by areas, since we divide radii by their sum. I would be grateful if you could ellaborate on that point (uniform distribution of random points inside the ellipse as proof of PDF correctness and uniqueness) – Euclides Jul 18 '23 at 06:59
  • in the meantime, I'll randomly generate points using the two other nonuniform PDFs I mentioned above. Just to see how their distribution looks like.............. – Euclides Jul 18 '23 at 07:03
  • OK. Meanwhile, I understood why the PDF $P_{nonuniform,2D}\left(\varphi\right) = \frac{b}{2\pi \left[ \left(b\cos\left(\varphi\right)\right)^2 + \sin\left(\varphi\right)^2 \right]}$ does not exhibit the ellipse shape in a polar plot. That's because we square the elliptical radius $r_{ellipse}$ to calculate the infinitesimal area element. If I use a constant radius of $1$ times the elliptical radius, I get the ellipse shape. However, the resulting expression does not satisfy the normalization condition. The appropriate normalization factor would be the integral over $\varphi$ of $r_{ellipse}$. – Euclides Jul 18 '23 at 11:19
  • I think this PDF with infinitesimal area element $dA = \frac{1}{2}r_{ellipse}r_{circle}d\varphi$ might be the correct one, since for the infinitesimal area element oriented at a given $\varphi$, its height (elliptical radius) does change, but the base remains constant, which, to me, indicates we should be using the infinitesimal arc length of the unit circle, including the unit radius. I could be wrong though. If I am right, then the correct PDF should be $P_{nonuniform,2D}\left(\varphi\right) = \frac{r_{ellipse}}{\int_{0}^{2\pi} r_{ellipse}}$............. – Euclides Jul 18 '23 at 11:32
  • and generalizing to an ellipsoid-like, nonuniform, three-dimensional PDF, we should have $P_{nonuniform,3D}\left(\vartheta,\varphi\right) = \frac{r_{ellipsoid}}{\int_{0}^{\pi}\int_{0}^{2\pi} r_{ellipsoid} d\varphi d\vartheta}$ – Euclides Jul 18 '23 at 11:41

1 Answers1

1

For $a>b>c>0$,

\begin{align} \begin{pmatrix} x \\ y \\ z \end{pmatrix} &= \begin{pmatrix} a\sin u \cos v \\ b\sin u \sin v \\ c\cos u \end{pmatrix} \\ dS &= abc\sqrt{\dfrac{x^2}{a^4}+\dfrac{y^2}{b^4}+\dfrac{z^2}{c^4}} \sin u \,du \, dv \\ S_{\text{total}} &= 2\pi \left[ c^{2}+\frac{bc^{2}}{\sqrt{a^{2}-c^{2}}}\, F\left( \cos^{-1} \frac{c}{a}, k \right)+b\sqrt{a^{2}-c^{2}}\, E\left( \cos^{-1} \frac{c}{a}, k \right) \right] \\ k &=\frac{a}{b}\sqrt{\frac{b^{2}-c^{2}}{a^{2}-c^{2}}} \\ P(u,v) &= \frac{abc\sin u}{S_{\text{total}}} \sqrt{\dfrac{x^2}{a^4}+\dfrac{y^2}{b^4}+\dfrac{z^2}{c^4}} \end{align}

Please refer to the case of elliptic arc in another post here.

Addendum

If you insist of using spherical polar coordinates, then

\begin{align} \begin{pmatrix} x \\ y \\ z \end{pmatrix} &= r \begin{pmatrix} \sin \theta \cos \phi \\ \sin \theta \sin \phi \\ \cos \theta \end{pmatrix} \\ \frac{1}{r(\theta, \phi)} &= \sqrt{ \frac{\sin^2 \theta \cos^2 \phi}{a^2}+ \frac{\sin^2 \theta \sin^2 \phi}{b^2}+ \frac{\cos^2 \theta}{c^2}} \\ P(\theta, \phi) &= \frac{|\partial_\theta \mathbf{r} \times \partial_\phi \mathbf{r}|}{S_\text{total}} \end{align}

which is tedious.

Ng Chung Tak
  • 18,990
  • @Ng Chung Tak: thanks for your help. I could only get back to this question today. However, I would prefer to first tackle the unit ellipse PDF. I found a contribution of yours here link and I have a question. How did you derive $dS$ from $r'$? I used $ds^2 = dr^2 + r^2d\varphi^2$, but I get a different result. – Euclides Dec 01 '23 at 13:54
  • Don't let $a=1$ but use the benefit of homogeneous in $a$ and $b$. Now simplify with care, we have the following. – Ng Chung Tak Dec 02 '23 at 04:33
  • $$\begin{align} S & \equiv \sin t \ C & \equiv \cos t \ \left( \frac{ds}{dt} \right)^2 &= r^2+\left( \frac{dr}{dt} \right)^2 \ &= \frac{a^2 b^2}{a^2S^2+b^2C^2}+ \left[ \frac{ab(b^2-a^2)SC}{(a^2S^2+b^2C^2)^{3/2}} \right]^2 \ & \equiv \frac{a^2 b^2 P}{(a^2S^2+b^2C^2)^3} \ P & \equiv (a^2S^2+b^2C^2)^2+(b^2-a^2)^2 S^2C^2 \ &= a^4S^4+2a^2b^2S^2C^2+b^4C^4+(a^4-2a^2b^2+b^4)S^2C^2 \ &= a^4 S^4+(a^4+b^4)S^2C^2+b^4C^4 \ &= a^4 S^2(S^2+C^2)+b^4C^2(S^2+C^2) \ &= a^4 S^2+b^4C^2 \end{align}$$ – Ng Chung Tak Dec 02 '23 at 04:33
  • @Ng Chung Tak: anyway, my result, reading as $dS_{ellipse} = \frac{b^2\left(b^4 + sin(\varphi)^2 - b^4sin(\varphi)^2\right)}{(b^2 + sin(\varphi)^2 - b^2sin(\varphi)^2)^{\frac{3}{2}}} d\varphi$, yields the same ellipse circumference, $S_{ellipse}$ (after integration over $\varphi$ between $0$ and $2\pi$) as if I use the expression you provided in the link above; and both results also match the two Ramanujan's approximations, especially for $b \geq \approx 0.4$. The resulting probability density function (PDF), $p(\varphi) = \frac{dS}{S}$ fulfills the normalization condition. – Euclides Dec 02 '23 at 14:13
  • I had a mistake in my original derivation for $dS_{ellipse}$ on Matlab. So, even though our expressions look different, they yield the same ellipse perimeter. So, probably they will become identical after some sort of rearrangement/ algebraic manipulation. Also, I forgot to mention that both perimeters and those of Ramanujan match that delivered by the complete elliptic integral of the second kind. So, the problem of the length of an infinitesimal element of the ellipse circumference is completely solved. I will update the expression for $dS_{ellipse}$ in my original question/ post. – Euclides Dec 02 '23 at 14:17
  • now, the next question is that, after all these rigorous derivations and implementations, a plot of the PDF still has the shape of the third plot (i.e., of the first plot for the ellipse PDF derivation part of the question) in my original question/ post. So, I am unsure if the PDF defined as $p(\varphi) = \frac{dS}{S}$ is actually conceptually rigorous. Shouldn't the PDF exhibit the shape of an ellipse? Since we are using ellipse-related quantities for its definition? Or only quantities following that PDF will exhibit the shape of an ellipse of given $b$? How is that? – Euclides Dec 02 '23 at 14:24