Just out of curiosity, I was wondering if anybody knows any methods (other than the integral test) of proving the infinite series where the nth term is given by $\frac{1}{n^2}$ converges.
Asked
Active
Viewed 9.0k times
15
-
1See http://math.stackexchange.com/questions/29450/self-contained-proof-that-sum-limits-n-1-infty-frac1np-converges-for – Argon Aug 22 '13 at 18:42
-
3Cauchy Condensation. Works for $\sum \frac{1}{n^p}$, $p\gt 1$. – André Nicolas Aug 22 '13 at 19:01
2 Answers
61
Hint: $$\frac{1}{n^2} < \frac{1}{n(n-1)}.$$
$$\frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} + \ldots + \frac{1}{n(n - 1)} = 1 - \frac12 + \frac12 - \frac13 + \ldots + \frac{1}{n - 1}-\frac1n = 1 - \frac1n \to 1.$$
njguliyev
- 14,473
- 1
- 26
- 43
16
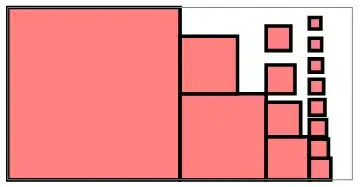
With fewer words. Hopefully clear enough. Oresme's style, but converging this time, and proving that the sum is $<2$.
J. W. Tanner
- 60,406
Jyrki Lahtonen
- 133,153
-
Do you happen to have a source for this? I'd like to see others like this if there is some central repository... – daniel Aug 22 '13 at 19:50
-
1I've seen it in some calculus book. I reproduced this with Mathematica. – Jyrki Lahtonen Aug 22 '13 at 19:50
-
-
May be, @Pedro. First I had no borders at all, then very thin ones, then way too thick. This is a compromise. I agree with you in the sense that the next stack would look horrible with this border thickness. Too bad I already closed the notebook. Also, there would be more orphaned images at imgur :-/ – Jyrki Lahtonen Aug 22 '13 at 20:03
-
2This is a very good illustration of the cauchy's condensation test that for a positive non-increasing function $f(n)$ the series $\sum f(n)$ and $\sum 2^{n}f(2^{n})$ converge/diverge together. – Paramanand Singh Oct 05 '13 at 10:44