Dual of the bilinear space vs. the bilinear space of dual spaces

Question

Let $X$, $Y$ be vector spaces (not necessarily finite dimensional) over field $k$. Is it always true $B(X,Y)^* \simeq B\left(X^*, Y^*\right)$? Here $B(X, Y)$ is the space of bilinear forms $b: X\times Y \to k$.

Background: On one hand, by the universal property of the tensor product, we have $B(X,Y)^*\simeq (X\otimes Y)^{**}$. Hence, through the canonical embendding into the bidual, we have embedding $X\otimes Y \hookrightarrow B(X,Y)^*$. On the other hand, map $x\otimes y\mapsto B_{x,y}\in B\left(X^*, Y^*\right)$ defined as $B_{x,y}(f,g):=f(x)g(y)$ is an embedding $X\otimes Y\hookrightarrow B\left(X^*, Y^*\right)$. When $X$ and $Y$ are of finite dimensions, the two embeddings are isomorphisms, and so we would have $B(X,Y)^* \simeq B\left(X^*, Y^*\right)$. My question concerns what happens when they are infinitely dimensional.

Thanks in advance.

Answer 1

I think the answer is no. The following content is mainly (almost just a copy of the highest voted and accepted answer) from https://mathoverflow.net/questions/56255/duals-and-tensor-products

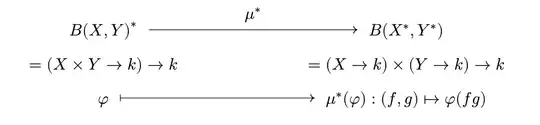
From $B(X,Y)^*\simeq (X\otimes Y)^{**}$ and $B(X^*,Y^*)\simeq (X^*\otimes Y^*)^{*}$. We just need to show that in general case $(X\otimes Y)^{*}$ does not (canonically) isomorphic to $X^*\otimes Y^*$. Usually one has the cannonical map $\mu: X^*\otimes Y^* \to (X\otimes Y)^{*}$ taking $\mu(f \otimes g)(x \otimes y)$ to $f(x)g(y)$. Hence the canonical map $\mu^*: B(X,Y)^* \to B(X^*,Y^*)$ taking $\phi: (X \times Y) \to k \to k $ to $\mu^*(\phi)(f, g)$ as $\phi(fg)$:

Next, we show (via an argument like Cantor's diagonal) that $\mu$ (and hence $\mu^*$) can be not an isomorphism in the infinite dimension case. Take $$X = Y = \bigoplus_{i \in \Bbb{N}} \Bbb{R}$$, i.e., the vector space consisting of all infinite sequences with only finite elements nonzero, as an example (In this case, their dual is the vector space consisting of all infinite sequences). And denote $$e_i = (0, \dots, 0, 1, 0, \dots)$$ be the element that only the $i$-th coordinate be $1$.

Let $\xi \in (X\otimes Y)^{*}$ define by taking $e_i \otimes e_j$ to $1$ if $i = j$ and otherwise to $0$. Then $\xi$ can not be the image of $\mu: X^*\otimes Y^* \to (X\otimes Y)^{*}$. Otherwise say $\xi = \mu(\sum_{k = 1}^r \phi_k \otimes \psi_k)$ with $\phi_k \in X^*$ and $\psi_k \in Y^*$. Then one has

$$ \xi(e_i \otimes e_j) = \sum_{k = 1}^r \phi_k(e_i)\psi_k(e_j) $$

and for any positive integer $n$,

$$ \{\xi(e_i \otimes e_j)\}_{1 \leq i, j \leq n} = \{\phi_k(e_i)\}_{1 \leq i \leq n, 1 \leq k \leq r} \cdot \{\psi_k(e_j)\}_{1 \leq k \leq r, 1 \leq j \leq n} $$

But for any $n > r$, the left-hand side matrix of the above equation, being the identity matrix, has rank $n$ the right-hand side matrix, being the product of two at most rank $r$ matrices, has at most rank $r$. And it's a contradiction. Hence $\mu$ is not surjective.

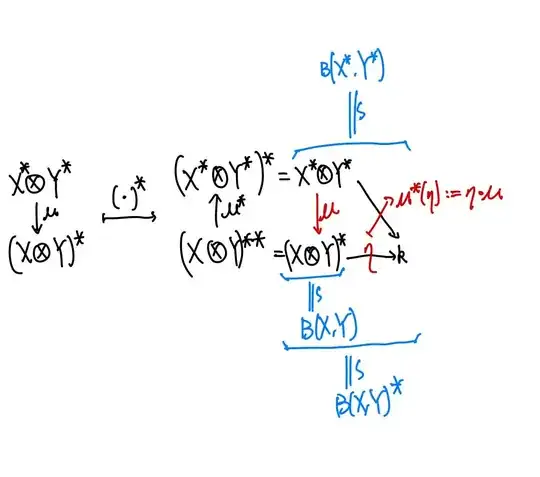
And for $\mu^*: B(X,Y)^* \to B(X^*,Y^*)$ the situation is similar, and the dual element $\xi^{*}$ of the above $\xi$ is mapped to zero by $\mu^*$. Hence it's not injective. (The relation between $\mu$ and $\mu^*$ is showed in the following hand-drawn diagram. Check this too: Dual spaces isomorphic, implies vector spaces itself are isomorphic? )

Besides the above content, they could be isomorphic not via the canonical map, since they could have the same cardinality of the basis. For this maybe see Why are infinitely dimensional vector spaces not isomorphic to their duals? (Usually we only care about the canonical map).