Calculation of Areas of Leaf-like Segments in an Equilateral Triangle

Question

I hope this message finds you well. I recently came across a captivating geometry problem involving an equilateral triangle and leaf-like segments formed by intersecting arcs. I encountered this problem in a competitive exam and have been trying to determine a precise analytical solution. After several attempts, I obtained varying results such as 2.112 or$\frac{3(\pi-2)}{8}$. Therefore, I am reaching out to seek your assistance in finding a definitive answer through an analytical or calculus-based approach.

Problem Description:

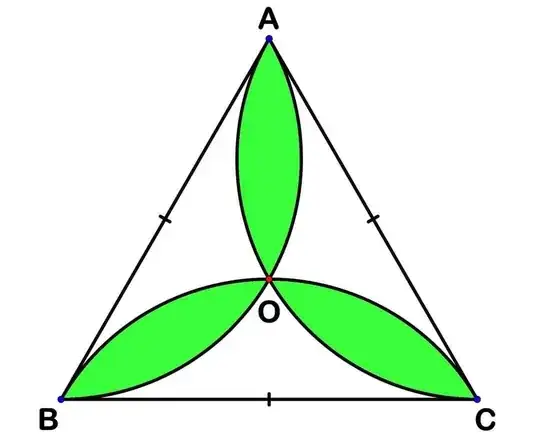
Consider an equilateral triangle ∆ABC, where each side measures 1 unit. Let O be the center of the triangle, where the arcs AOB, BOC, and COA intersect. The objective is to calculate the sum of the areas of the leaf-like green segments formed by these arcs within the triangle.

Approach:

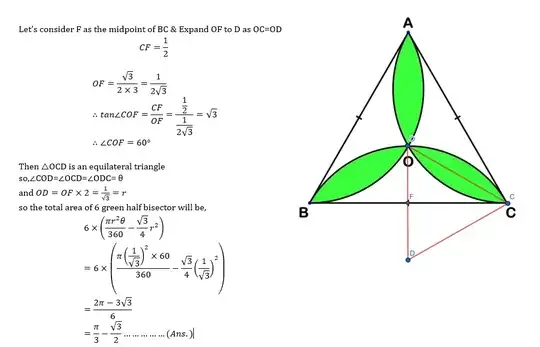
I have attempted to solve this problem analytically, but my results have been inconsistent. Consequently, I would greatly appreciate your expertise in helping me find a precise solution using rigorous mathematical techniques, such as calculus or other applicable methodologies.

Expected Outcome:

By collaborating on this problem, I aim to derive a definitive answer for the sum of the areas of the leaf-like segments formed by the arcs within the equilateral triangle. This solution will not only enhance my understanding of geometry but also serve as a valuable resource for others facing similar challenges.

I am grateful for your time and expertise, and I look forward to your insightful responses. Please let me know if any further clarifications or additional information is required to assist you in addressing this problem effectively.

Thank you in advance for your support!

No need to resort to calculus here. You can do this with geometry; here are some hints: 1) what is the radius of the arcs that define the green regions? Where are the centres of these arcs? 2) What angle is swept out by one of the arcs between $A$ and $B$? Between $A$ and $O$? 3) Draw the line $AO$ to divide the top green region into a left half and a right half. Use the above to work out the area of one of these halves (it's a segment of a circle). 4) multiply up by the number of such halves in the diagram — Chris Lewis, Jul 14 '23 at 16:48
Does this answer your question? Area of enclosed overlapping circles within an equilateral triangle - this is Alv's comment's suggestion. Of course, since the side length's here are $\sqrt{6}$ smaller, the answer for the area in this particular equilateral triangle will be $6$ times smaller. — John Omielan, Jul 14 '23 at 17:41

score 1 · Accepted Answer · answered Jul 14 '23 at 18:25

1

By all suggestion, I can come up with this solution

I shall remain grateful to you if give check this for me please.

answered Jul 14 '23 at 18:25

Raihan Sarker

522

Calculation of Areas of Leaf-like Segments in an Equilateral Triangle

1 Answers1