0

The analogy between arthimetic and CT concept is used ubiquitous by a book done one of the very founders of CT themself called Conceptual Mathematics. I found this quite profound and made a post paraphrasing what was written in one of those pages see here. Here is another example I found when reading about categorical sections:

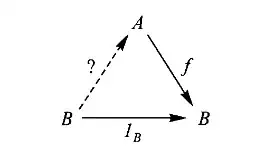
The first proposition may be regarded as an analog for maps to the observation that once we have multiplication and ‘reciprocals’ (numbers like x =} to solve equations like $3x=1$) we can then express the answers to more general division problems like $3x=5$ by $x= \frac{5}{3}$. The proposition says that if the single choice problem

enter image description here

has a solution( a section for f ) , then every choice problem

enter image description here > involving this same $f$ has a solution

Is there a way to make this connection concrete?

tryst with freedom
  • 11,538
  • The elements of a monoid (such as the multiplicative group of real numbers) can be viewed as the morphisms of a category with only one object. Is that what you're looking for? – Karl Jul 04 '23 at 17:23
  • 2
    Does CT mean "category theory"? (guessing by the tag used) My two cents are that it'd be better to type it: i've never seen that abbreviation used and there's no charge for characters. – rschwieb Jul 05 '23 at 13:50

0 Answers0